Наращение по сложным процентам

В среднесрочных и долгосрочных финансово-кредитных операциях в случае, если проценты не выплачиваются сразу после их начисления, а присоединяются к сумме долга, для наращения применяются сложнее проценты. База для начисления сложных процентов увеличивается с каждым периодом выплат. Присоединение начисленных процентов к сумме долга, которая служит базой для их начисления, называется капитализацией процентов.

Предположим, что клиент положил в банк сумму, равную 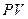рублей под процентную ставку 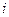. Через один период наращения (например, через год) на его счете будет сумма, равная 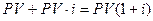. Полученная сумма может быть вновь инвестирована под процентную ставку 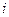на следующий процентный период. Тогда к концу второго процентного периода на его счете будет сумма, которая может быть исчислена следующим образом: 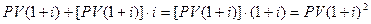. Если повторить этот процесс еще раз, то к концу третьего процентного периода на счете будет сумма, которую можно определить следующим образом:

.

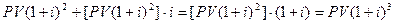Нетрудно видеть, что наращение по сложным процентам описывается геометрической прогрессией, начальный член которой , а знаменатель .

Тогда 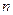-ый член прогрессии, определяющий величину накопленной к концу 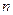- го периода суммы 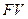, определяется по формуле: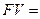

Следовательно, формула для расчета наращенной суммы в конце 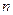-го года при условии, что проценты начисляются один раз в году, имеют вид:

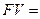
, (3.1)

где 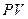-первоначальный размер долга,

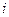-процентная ставка,

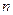-число лет наращения.

Проценты за этот период ( 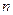лет) равны:

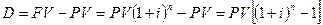
Величина называется множителем наращения по сложным процентам. Для облегчения расчетов со сложными процентами составлены таблицы множителей наращения и множителей дисконтирования.

Пример. Какой величины достигнет долг, равный 1000 000 рублей, через 5 лет при росте по сложной ставке 15,5% годовых?

Решение: PV= 1000 000 рублей;i = 0,155; n=5.