Математическое дисконтирование по простым процентам
В финансовой практике часто приходится решать задачу, обратную вычислению наращенной суммы, которая может быть сформулирована таким образом: определить сумму 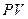 , которую необходимо инвестировать в данный момент времени, с тем, чтобы через некоторый определенный период
, которую необходимо инвестировать в данный момент времени, с тем, чтобы через некоторый определенный период 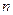 получить при установленной ставке процента
получить при установленной ставке процента 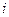 требуемую наращенную сумму
требуемую наращенную сумму 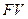 . Для решения этой задачи применяется операция дисконтирования.
. Для решения этой задачи применяется операция дисконтирования.
Дисконтирование позволяет по известным наращенной сумме, процентной ставке и сроке финансовой операции определить современную стоимость этой наращенной суммы.
Другими словами дисконтирование позволяет определить, какую первоначальную сумму надо дать в долг, чтобы получить в конце срока сумму 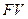 при условии, что на долг начисляются проценты по ставке
при условии, что на долг начисляются проценты по ставке 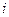 .
.
В зависимости от вида процентной ставки применяются два вида дисконтирования: математическое дисконтирование и банковский (коммерческий) учет. В первом случае при расчете применяют обычные (декурсивные), а во втором – авансовые проценты.
Рассмотрим, как производится математическое дисконтирование.
Выразив из формулы (2.1) 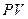 , получим формулу математического дисконтирования:
, получим формулу математического дисконтирования:
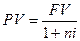 ,(2.5)
,(2.5)
Здесь 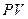 - современная стоимость наращенной (будущей) суммы денег
- современная стоимость наращенной (будущей) суммы денег 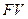 ;
; 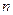 - срок проведения финансовой операции (число процентных периодов);
- срок проведения финансовой операции (число процентных периодов); 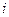 - процентная ставка.
- процентная ставка.
Дисконтный множитель 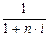 показывает, какую долю составляет первоначальная величина долга
показывает, какую долю составляет первоначальная величина долга 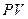 в его окончательной сумме
в его окончательной сумме 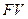 .
.
Пример. Заемщик должен возвратить кредит единовременным платежом с процентами за период 2 года. Проценты по кредиту составили 12% годовых. Какую сумму получил заемщик в момент заключения кредитного договора и чему равен дисконт, если сумма к возврату составляет 1 500 000 рублей?
Решение: FV=1500 000 рублей; n=2 года; i= 0,12
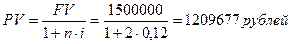 ,
,
 .
.
В случае если срок финансовой операции задан в днях или в месяцах, из формулы (2.2) получим формулу математического дисконтирования для 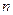 <1:
<1:

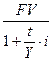 , (2.6)
, (2.6)
где 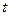 - длительность финансовой операции в днях (в месяцах);
- длительность финансовой операции в днях (в месяцах);  - число дней (месяцев в году).
- число дней (месяцев в году).
Пример. Какую сумму инвестор должен внести сегодня под 16% годовых, чтобы через 180 дней после подписания договора накопить 310 тыс. руб. при условии, что начисляются простые точные проценты.
n Решение: FV=310 000 рублей; t=180 дней; i=0,16; Y=365 дней.
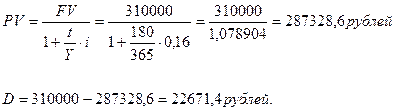
Дата добавления: 2015-10-26; просмотров: 2412;
