Теоремы сложения вероятностей
Теорема сложения вероятностей. Пусть А и В – случайные события, тогда P(A+ B)=P(A)+P(B)-P(AВ).
Следствие 1 (теорема сложения вероятностей для несовместных событий). Пусть события А1, А2, …, Аn несовместны, тогда вероятность их суммы равна сумме их вероятностей, т.е.
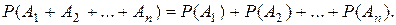
Следствие 2. Пусть события А1, А2, …, Аn образуют полную группу, тогда сумма их вероятностей равна 1:
.
 |
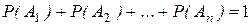Два события, образующие полную группу называются противоположными.Противоположное событие к событию А обозначается через
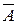. Отметим следующие свойства противоположных событий:
1) Ø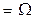 
,
2) 
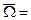Ø,
3) 
,
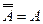4) 
,
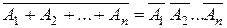5) 
.
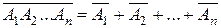Следствие 3. Вероятность противоположного события к событию А равна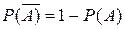 
.
Дата добавления: 2015-10-21; просмотров: 720;