Образы и прообразы множеств при отображениях
Пусть задана функция 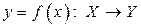 и задано множество
и задано множество 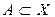 .
.
Образом множества А при отображении fназывается множество всех 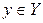 , являющихся значениями функции f в точках
, являющихся значениями функции f в точках 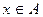 .
.
Обозначение: 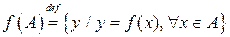 .
.
В частности, 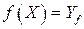 , то есть образом множества задания функции является множество ее значений.
, то есть образом множества задания функции является множество ее значений.
Если множество 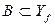 , то множество A всех значений аргумента х, для которых
, то множество A всех значений аргумента х, для которых 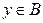 , называется прообразом множества В при отображении f. Записать кратко определение прообраза можно так:
, называется прообразом множества В при отображении f. Записать кратко определение прообраза можно так:
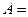
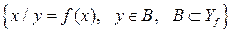 .
.
Пример 4 (образы и прообразы множеств при различных отображениях)
1) Множество 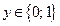 является образом множества
является образом множества 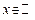 при отображении функцией
при отображении функцией
Дирихле; множество 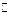 является прообразом множества
является прообразом множества 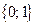 при отображении той же функцией;
при отображении той же функцией;
2) 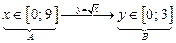
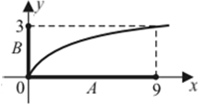
| 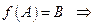 В — это образ множества А при отображении функцией В — это образ множества А при отображении функцией 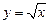 ,
A — это прообраз множества B при этом отображении функцией ,
A — это прообраз множества B при этом отображении функцией 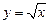 ; ;
|
3) найдем образ множества 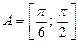 при отображении функцией
при отображении функцией 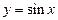 :
:
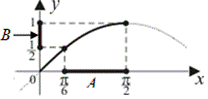
| 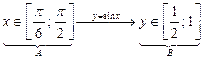 ,
то есть ,
то есть 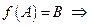 В — это образ мно- жества А при отображении функцией В — это образ мно- жества А при отображении функцией 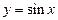 ; ;
|
4) найдем образ множества 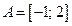 при отображении функцией при отображении функцией 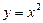 . .
|
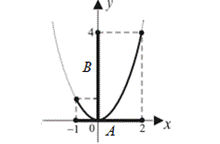
| 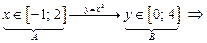
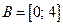 или или 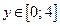 — это образ множества А при отображении функцией — это образ множества А при отображении функцией 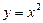 ; ;
|
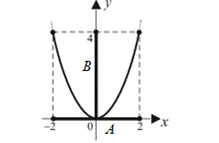
5) найдем прообраз множества 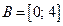 при отображении функцией
при отображении функцией 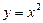 :
:
| 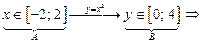
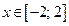 — это прообраз множества В при отображении функцией — это прообраз множества В при отображении функцией 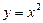 . .
|
Дата добавления: 2015-10-19; просмотров: 11658;
