Определение отображения множеств
Наряду с понятиями множества и элемента множества в математике первичным понятием является понятие соответствия. Это понятие присутствует неявным образом при описании понятия множества: каждому из элементов поставлено в соответствие некоторое свойство, позволяющее судить о том, является ли этот элемент элементом данного множества или нет. Среди всевозможных соответствий важнейшими в математике являются функции, или отображения множеств.
| Определение отображения множеств или функции |
Пусть заданы непустые множества Xи Y. Соответствие, при котором каждому элементу 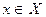 соответствует единственный элемент соответствует единственный элемент 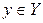 , называется отображением множества X в множество Y или функцией, определенной на множестве X и принимающей значения в множестве Y. , называется отображением множества X в множество Y или функцией, определенной на множестве X и принимающей значения в множестве Y.
|
Иллюстрация к понятию отображения множества Xв множество Y, то есть к понятию функции приведена на рис. 28.
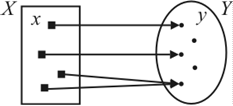 Рис. 28
Рис. 28
| каждому элементу 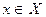 поставлен в соответствие единственный элемент поставлен в соответствие единственный элемент 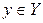 . .
|
Пример 1 (соответствия, не являющиеся функциями)
| 1) | 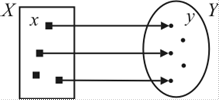
| не каждому элементу 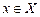 поставлен в соответствие элемент поставлен в соответствие элемент 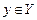 ; ;
|
| 2) | 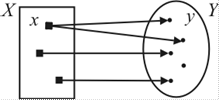
| хотя бы одному элементу 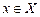 поставлены в соответствие два элемента поставлены в соответствие два элемента 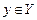 . .
|
Обозначения для отображения множеств, или функции
Отображение множеств, или функция обозначается одним из следующих способов:
§ 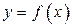 , , 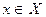 ; ;
| § 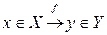 ; ;
| § 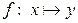 , , 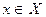 , , 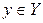 ; ;
| ||
§ 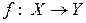 ; ;
| § 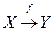 . .
|
При этом элемент 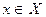 называется независимой переменной, или аргументом функции; соответствующий ему элемент
называется независимой переменной, или аргументом функции; соответствующий ему элемент 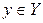 называется зависимой переменной; говорят, что между элементами x и y существует функциональная зависимостьf.
называется зависимой переменной; говорят, что между элементами x и y существует функциональная зависимостьf.
Множество X называется множеством задания функцииf (или множеством определения f). Множество тех элементов 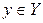 , каждый из которых поставлен в соответствие хотя бы одному элементу
, каждый из которых поставлен в соответствие хотя бы одному элементу 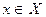 , называется множеством значений функцииf и обозначается
, называется множеством значений функцииf и обозначается 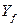 :
:
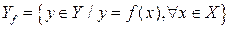 .
.
Очевидно, что 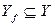 , то есть множество значений функции является подмножеством множества Y, в частности,
, то есть множество значений функции является подмножеством множества Y, в частности, 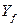 может совпадать с Y.
может совпадать с Y.
Пример 2 (отображение множеств)
1) X — множество треугольников на плоскости,
Y — множество положительных действительных чисел;
площадь треугольника S — это есть функция, определенная на множестве X и принимающая значения в множестве Y, или отображение множества X в множество Y, то есть 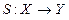 ;
;
если Р – это периметр треугольника, то 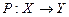 ;
;
если M – это длина наибольшей медианы треугольника, то 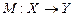 ;
;
2) функция 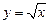 :
:
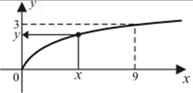
| 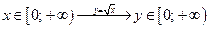 ; ; 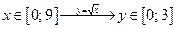 ; ;
|
3) функция 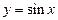 :
:
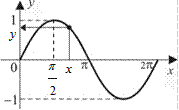
| 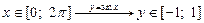 ; ; 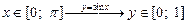 ; ; 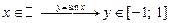 ; ;
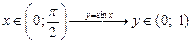 ; ;
|
4) последовательность с общим членом 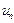 есть функция, отображающая множество натуральных чисел
есть функция, отображающая множество натуральных чисел 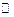 в множество действительных чисел
в множество действительных чисел 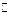 ;
;
например, 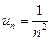 :
: 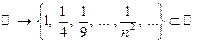 ;
;
5) функция Дирихле: 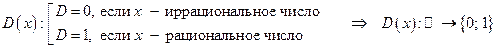 .
.
Дата добавления: 2015-10-19; просмотров: 1617;
