Основные типы отображений
Рассмотрим отображение 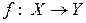 .
.
1. Если множество значений функции 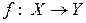 совпадает с множеством Y, то есть
совпадает с множеством Y, то есть  , то отображение f называется отображением множества X на множество Y, или сюръекцией.
, то отображение f называется отображением множества X на множество Y, или сюръекцией.
2. Если в отображении 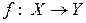 разным элементам
разным элементам 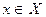 соответствуют разные элементы
соответствуют разные элементы 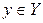 , то есть при
, то есть при 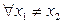 будет
будет 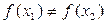 , то отображение множества X в множество Y называется инъекцией.
, то отображение множества X в множество Y называется инъекцией.
3. Если отображение 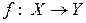 является одновременно сюръекцией и инъекцией, то оно называется биекцией.
является одновременно сюръекцией и инъекцией, то оно называется биекцией.
Иллюстрации к разным типам отображений приведены на рис. 29-31.
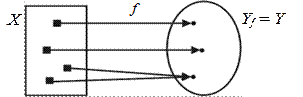 Рис. 29
Рис. 29
| сюръекция 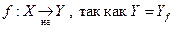
| |
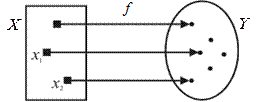 Рис. 30
Рис. 30
| инъекция 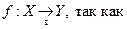 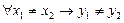
| |
 Рис. 31
Рис. 31
| биекция 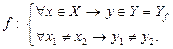
|
Очевидно, что биективное отображение 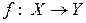 является взаимно однозначным отображением, то есть выполняются следующие условия:
является взаимно однозначным отображением, то есть выполняются следующие условия:
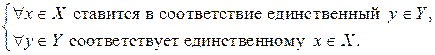
Пример 3 (отображения разных видов)
1) 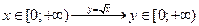 — биекция;
— биекция;
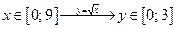 — биекция;
— биекция;
2) 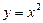 
| 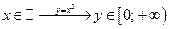 — сюръекция, но не инъекция; — сюръекция, но не инъекция;
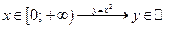 — инъекция, но не сюръекция; — инъекция, но не сюръекция;
 — сюръекция и инъекция, то есть биекция; — сюръекция и инъекция, то есть биекция;
|
3) функция Дирихле 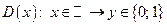 — сюръекция, но не инъекция, следовательно, не биекция.
— сюръекция, но не инъекция, следовательно, не биекция.
Дата добавления: 2015-10-19; просмотров: 2874;
