Обратное отображение
Пусть имеем отображение общего вида 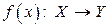 , причем
, причем 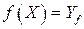 , где
, где 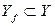 , (рис. 33).
, (рис. 33).
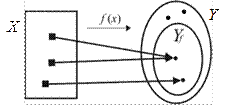
Рис. 33
Если рассмотреть отображение 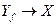 , то оно называется обратным отображениемпо отношению к отображению
, то оно называется обратным отображениемпо отношению к отображению 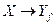 . Понятно, что обратное отображение является, вообще говоря, многозначным.
. Понятно, что обратное отображение является, вообще говоря, многозначным.
Если отображение  является взаимно однозначным (биективным), то обратное ему отображение
является взаимно однозначным (биективным), то обратное ему отображение 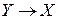 является также взаимно однозначным отображением множества
является также взаимно однозначным отображением множества 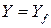 на множество X, (рис. 34); в этом случае обратное отображение определяет функцию
на множество X, (рис. 34); в этом случае обратное отображение определяет функцию 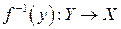 , которая называется обратной функциейпо отношению к функции
, которая называется обратной функциейпо отношению к функции 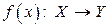 .
.
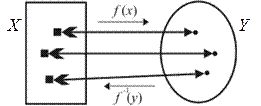 Рис. 34
Рис. 34
| если 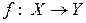 — биекция, то — биекция, то 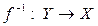 — тоже биекция. — тоже биекция.
|
Очевидно, что функция 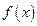 является обратной по отношению к функции
является обратной по отношению к функции 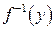 , а обе эти функции f и
, а обе эти функции f и  называются взаимно обратными функциями.
называются взаимно обратными функциями.
Пример 5 (взаимно обратные функции)
| 1) | 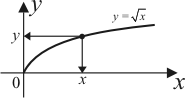
| 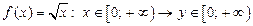 и
и 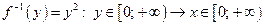 ; ;
|
| 2) | 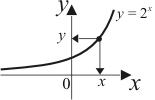
| 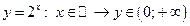 и
и 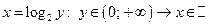 . .
|
Подробнее о взаимно обратных функциях изложено в §8 данного конспекта.
Дата добавления: 2015-10-19; просмотров: 2839;
