БИНАРНЫЕ ОТНОШЕНИЯ НА МНОЖЕСТВЕ

Отношение 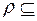А А 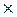называется отношением на A. Такие отношения называются также бинарными отношениями на множестве A. То есть отношение на A - это отношение между элементами одного и того же множества A.

Для таких отношений можно выделить несколько специальных свойств.

1. Рефлексивность

Отношение 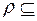А 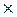А является рефлексивным, если
.

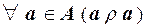Простейшее рефлексивное отношение на A - это множество, состоящее из всех пар вида (a, a), где a 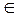A. Такое отношение называется единичным отношением или диагональю и обозначается как e.

2. Симметричность

Отношение 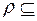А 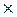А - является симметричным, если
" a, bÎ A (ar bÞ br a).

То есть отношение 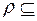А 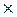А симметрично, если для любых a и b из того что (a, b)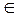 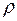следует, что пара (b, a) .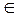

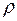Поэтому отношение r несимметрично, если хотя бы для одной пары (a, b) не выполняется указанное свойство. Нетрудно видеть, условие симметричности равносильно условию:

" a, bÎ A (ar bÛ br a).

3. Антисимметричность

Отношение 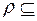А 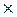А- антисимметричное, если

"a,bÎ A(ar b & br a Þa= b).

То есть отношение 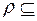А 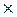А является антисимметричным, если из (a, b)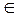 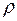и (b, a)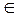 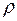следует, что a = b.

Заметим, что антисимметричность представляет свойство несимметричности в сильной форме. Отношение антисимметрично, если оно несимметрично всюду за исключением пар из единичного отношения e. При этом не требуется, чтобы в антисимметричном отношении содержались все пары, компоненты которых совпадают. Поэтому существуют отношения, которые являются симметричными и антисимметричными одновременно. Такие отношения составлены парами, имеющими равные первую и вторую компоненты.

4. Транзитивность

Отношение 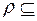А 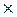А- транзитивное, если

"a, b, cÎ A(ar b & br c Þar c).

Отношение 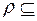А 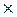А является транзитивным если из (a, b) 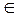r и
(b, c) 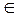r следует, что (a, c) 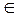r. Содержательно транзитивность состоит в том, что если осуществляется последовательный многократный переход между элементами множества A, по связям отношения r, то между первым и последним элементами такого перехода также выполняется отношение r.

Упражнение. Доказать следующие свойства отношений:

1) 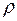- рефлексивное 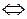e Í r;

2) r - симметричное 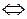r = r^-1;

3) r - антисимметричное 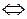r Ç r^-1Í e;

4) r - транзитивное 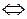r r Í r.

Упражнение. Является ли транзитивным бинарное отношение, на множестве {a, b, c, d, e, f} заданное диаграммой:

a d

b e

c f

Рассмотрим несколько примеров отношений на множестве.

Пусть A - это множество всех людей.

Отношение r = "дружить". Для этого отношения справедливость условия (a, b) 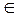r означает, что a дружит с b. Это отношение симметричное, но оно нетранзитивное и нерефлексивное.

Отношение "любить" - несимметричное и нетранзитивное, но, по-видимому, рефлексивное.

Отношение "быть родственником" - рефлексивное, симметричное и транзитивное.

Отношение "руководить" - антисимметричное, транзитивное и нерефлексивное.

Если 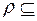А 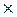А - некоторое отношение, то рефлексивным, симметричным, транзитивным замыканиями этого отношения называются минимальные отношения на А, которые содержат r и являются соответственно рефлексивными, симметричными и транзитивными.