Доказательство. Разобьем доказательство теоремы на несколько этапов.
Разобьем доказательство теоремы на несколько этапов.
1. Построение разбиения, порождаемого отношением r.
Пусть r - отношение эквивалентности на множестве A.
Для каждого x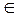 
A обозначим как [x] множество {y½xry}. Поскольку отношение r рефлексивно, то x Î [x], а, значит, каждое множество [x] является непустым и система множеств [x], где x Î A, содержит все элементы A. Из семейства множеств {[x]| x ÎA } удалим кратные вхождения одинаковых множеств. В результате получим семейство непустых несовпадающих множеств R, в которых содержатся все элементы A.
2. Обоснование того, что R образует разбиение.
Пусть [x] и [y] - произвольные классы из семейства R. Покажем, что они либо не пересекаются, либо совпадают, т.е. возможны только два случая:
1) [x] Ç [y] =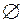 
;
2) [x] Ç [y] 
.
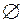Предположим, что это свойство является неверным. То есть для некоторых двух элементов x и y множества [x] и [y] пересекаются, но не совпадают (рис 3.1).
[x] [y]
x z y
ab
Рис.3.1
Здесь z - это элемент, общий для классов [x] и [y], аa и b - произвольные элементы в [x] и [y] соответственно.
1. Докажем, что [x] 
[y]. Пусть x r a. Покажем, что
справедливо отношение y r a:
a) поскольку x r z, то из симметричности r следует, что
z r x;
b) поскольку z r x и x r a, то из транзитивности r вытекает, что z r a;
c) из y r z и z r a и транзитивности r имеем y r a. Поэтому aÎ[y], а, значит, [x] [y].
2. Обратное включение [y] [x] может быть доказано, если повторить проведенные рассуждения, поменяв в них местами x и y, а также aи b.
Следовательно, справедливо равенство множеств [x] и [y]. Последнее противоречит предположению о том, что эти множества являются разными.
Это означает, система множеств R образует разбиение множества разбиение A.
3. Обоснование того, что R разбивает A на классы эквивалентных элементов.
3.1. Покажем, что в каждом классе из R любые два элемента находятся между собой в отношении r.
Пусть выбраны произвольное множество [x] Î R и элементы a, b Î A. Покажем, что ar b. Действительно, по определению множества [x] справедливы соотношения: xraи xrb. Из соотношения xraи симметричности r следует, что arx. Из arx и xrb, а также транзитивности r следует, что arb.
3.2. Покажем, что элементы из разных классов в R не находятся в отношении r. Пусть [x], [y] Î R и aÎ[x], bÎ[y] - произвольные элементы этих множеств. Покажем, что (a, b) Ï r. Предположим противное. Пусть arb. Тогда из симметричности отношения r следует, что bra. Поскольку yrb и bra, то из транзитивности r следует, что yra. Поэтому aÎ[y]. Последнее противоречит тому, что множества [x] и [y] не пересекаются.
Следовательно, (a, b) Ï r.
Дата добавления: 2015-09-18; просмотров: 524;