ОПРЕДЕЛЕНИЕ. Элемент a называется наибольшим (наименьшим) в отношении r, если " bÎ A(ar b) (" aÎ A(br a)).

Элемент a называется наибольшим (наименьшим) в отношении r, если " bÎ A(ar b) (" aÎ A(br a)).

Понятно, что всякое упорядоченное множество имеет не более одного наибольшего (наименьшего) элемента. Например, если A - это множество возможных ситуаций или вариантов, из которых требуется выбрать оптимальный, и r - отношение предпочтения одних вариантов перед другими, представляющее собой отношение порядка, то наибольший и наименьший элементы упорядоченного множества (A, r) представляют соответственно наилучший и наихудший варианты.

В общем случае упорядоченное множество может не иметь наибольшего или наименьшего элементов. Например, это так для отношения порядка, диаграмма которого приведена на рис 3.2.

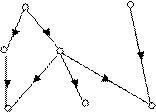a b

cd

E f g

Рис. 3.2.

Здесь элементы a и b не являются наибольшими, обладают свойством максимальности для всех тех элементов A, с которыми они находятся в отношении r.