ОПРЕДЕЛЕНИЕ. Пусть А B. Тогда отношение {(y, x)|(x, y)Îr} называется отношением, обратным к отношению r.

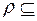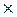Пусть А B. Тогда отношение {(y, x)|(x, y)Îr} называется отношением, обратным к отношению r.

Для обозначения отношения, обратного к r, применяется запись r^-1.

Понятие обращения отношений есть обобщение понятия обратного отображения. При этом обратное отношение всегда существует. Поскольку (r^-1)^-1= r, то отношения и их обращения находятся в биективной зависимости. Поэтому обращение всякого отношения порождает в общем случае новое отношение, которое совпадает с ним с точностью до простого преобразования.

Например, рассмотрим отношение управления людьми руководит Í A ´ A, где A - множество людей, определяемое соотношением: arb Û a руководит b.

Тогда отношение, обратное к отношению руководит, можно назвать словом руководим. Такое название соответствует содержательному смыслу обратной связи между b и a.

Понятие отношения может быть обобщено на произвольное конечное семейство множеств А₁, .., А_k следующим образом.

Отношением на произвольном числе множеств А₁, ... , А_k является всякое множество 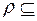А₁ 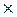... А_k. Однако отношения на парах множеств являются практически наиболее часто используемыми отношениями. Во многих случаях через такие отношения, с помощью специальных комбинаций отношений, могут выражаться отношения над более чем двумя множествами.