Доказательство. Действительно, пусть (a, d)
1. Покажем, что  (
( 
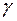 )
)  (
( 
 )
) 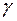 .
.
Действительно, пусть (a, d) 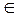
 (
( 
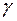 ), т.е. существует b такое, что a a b и b(
), т.е. существует b такое, что a a b и b( 
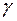 )d. Тогда существует такое с, что b
)d. Тогда существует такое с, что b  с и с
с и с 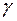 d. Поэтому a(
d. Поэтому a( 
 )с. Это означает, что a((
)с. Это означает, что a(( 
 )
) 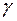 )d. Следовательно, справедливо включение
)d. Следовательно, справедливо включение  (
( 
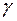 )
)  (
( 
 )
) 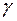 .
.
2. Покажем, что ( 
 )
) 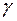 )
) 
 (
( 
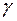 ).
).
Пусть (a, d) 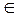 (
( 
 )
) 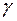 . Тогда существует такое с, что
. Тогда существует такое с, что
a ( 
 )с и с
)с и с 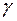 d. Поэтому найдется такой элемент b, для которого справедливы соотношения: a
d. Поэтому найдется такой элемент b, для которого справедливы соотношения: a  b и b
b и b  с. Поэтому b(
с. Поэтому b( 
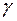 )d, т.е. a
)d, т.е. a  (
( 
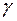 )d.
)d.
Следовательно, имеет место включение множеств:
( 
 )
) 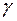

 (
( 
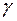 ) .
) .
Значит,  (
( 
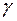 ) = (
) = ( 
 )
) 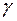 .
.
Дата добавления: 2015-09-18; просмотров: 671;
