ОПРЕДЕЛЕНИЕ И ПРИМЕРЫ ОТНОШЕНИЙ

Содержательно всякое отношение состоит из таких пар элементов, между которыми существует определенная смысловая связь. Например, пусть А - это множество людей, а B - множество наименований специальностей. Тогда множество всех таких пар, в которых первая компонента задает конкретного человека, а вторая - специальность, которой такой человек владеет, образует отношение на А 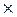B. Для обозначения отношений в дальнейшем будут использоваться строчные символы греческого алфавита: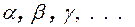

Если (a, b) 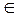r, то в этом случае говорят, что элементы a и b находятся между собой в отношении r.

Для записи факта, что элементы a и b находятся между собой в отношении r, используется также запись arb.

Одним из свойств бинарных отношений на произвольных множествах А и B является возможность взаимно однозначного соответствия между такими отношениями и бинарными предикатами, переменные которых принимают значения из множеств А и B соответственно.

Такое соответствие предикатов и отношений определяется следующими соотношениями.

1. Пусть r Í А 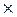B. Ему соответствует такой предикат P(x, y), для которого переменные x и y принимают значения на множествах A и B, что P(x, y) является истинным для тех и только тех наборов значений переменных x и y, которые входят в отношение r.

2. Пусть P(x, y) - некоторый предикат, переменные которого принимают значения из множеств A и B соответственно. Этому предикату можно сопоставить отношение r Í А ´ B, состоящее из тех и только тех элементов множества А B, на которых предикат Pявляется истинным.

Понятие отношения обобщает понятие отображения.

Если 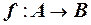- некоторое отображение, то ему можно поставить в соответствие отношение 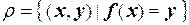. Такое отношение r принято называть графиком отображения f.

Если отношение r образует график некоторого отображения, то для него справедливо следующее свойство. Для каждого элемента x 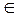A в отношении r содержится ровно одна пара, первая компонента которой равна x.

Отношения, для которых не выполнено последнее свойство, не являются графиками отображений. В этом случае имеет место один из случаев:

1) для некоторого a 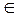A в r нет пары с первой компонентой, равной a;

2) для некоторого a 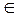A в r содержится не менее двух разных пар, первая компонента которых равна a.