Доказательство. Пусть a - это произвольный элемент, входящий в Ai .

Пусть a - это произвольный элемент, входящий в 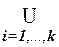A_i .

Покажем, что в левой и правой частях равенства (1) этот элемент множества A учитывается ровно один раз.

Для левой части (1) очевидно, что это так.

Рассмотрим правую часть доказываемого равенства. Предположим, что a содержится в r разных множествах из множеств A₁, ... , A_k. Тогда:

- в n₁ элемент a учтен 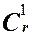раз;

- в n₂ элемент a учтен 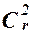раз;

. . .

- в n_r элемент a учтен 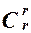раз.

В последующих слагаемых правой части (1) элемент a не учитывается ни разу.

Поэтому в выражении:

n₁ +... + (-1)^i-1 n_i+ ...+(-1)^k-1n_k

элемент aучтен ровно

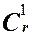+ ... + (-1)^i-1 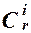+ ... + (-1)^r-1 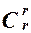раз.

Докажем равенство:

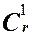+ ... + (-1)^i-1 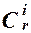+ ... + (-1)^r-1 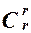= 1.(2)

Перенесем все члены этого равенства в правую часть и с учетом того, что 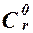= 1, получим:

0= 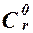- 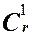+ ... + (-1)ⁱ 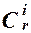+ ... + (-1)^r 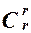. (3)

Воспользуемся формулой бинома Ньютона:

(1 - x)^r = 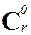- 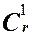x+... + (-1)ⁱ 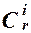xⁱ +...+(-1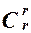)^r x^r.

Очевидно, что формула (3) - частный случай бинома Ньютона для x = 1.

Значит, равенство (2) является справедливым. Поэтому элемент a учитывается в правой части формулы (1) ровно один раз.