РАЗБИЕНИЯ МНОЖЕСТВ НА ЧАСТИ

Пусть задано множество S = {a₁, ... , a_n}. Требуется распределить элементы S по k именованным множествам S₁, ... , S_kтак чтобы в S₁ попало n₁ элементов, в S₂ - n₂ элементов, . . . , в S_k - n_k элементов множества S. При этом всякий элемент множества S попадает лишь в одно из множеств S₁, ... , S_k.

Поэтому справедливы соотношения:

S = 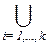S_i и n = 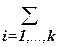|S_i |.

Такое распределение элементов S среди множеств S₁, ... , S_k называется разбиением S на части, имеющие заданные мощности. При этом множества, на которые разбивается S, являются именованными, то есть различаются не только по составу, но и по именам. Поэтому в задаче разбиения S на части важно не только выделение систем подмножеств с заданными мощностями, на которые распадается исходное множество, но и то какие множества образуют какие части.

Рассмотрим несколько примеров задач, приводящих к разбиениям множеств на части.

1. Имеется 15 разных картин, которые требуется разместить в трех залах музея так, чтобы в первом зале было выставлено 6 картин, во втором - 5 картин, в третьем - 4 картины.

Всякое распределение картин по залам, с выполнением сформулированных условий, является разбиением множества из 15 картин на три части, мощности которых равны соответственно 6, 5, 4.

2. Требуется распределить 20заданий поровну между пятью служащими.

Любое распределение заданий представляет собой разбиение множества всех заданий на 5 подмножеств, каждое из которых содержит четыре элемента.

Выведем формулу для нахождения числа различных разбиений конечного множества на части.

Пусть задано множество S = {a₁, ... , a_n}, которое требуется разбить на k подмножеств S₁, ... , S_k, содержащих соответственно по n₁, . . . , n_k элементов.

Возьмем произвольную перестановку a_i1, . . . , a_in элементов S. Для этой перестановки определим разбиение S на части, полагая, что первые n₁ элементов в ней образуют множество S₁, следующие за ними n₂ элементов перестановки образуют S₂ и т.д. Последние n_k элементов перестановки образуют множество S_k. Приведённое правило определяет отображение множества перестановок элементов S во множество разбиений S на части.

Определим свойства этого отображения.

Пусть множества S₁, ... , S_k образуют разбиение S на части с заданными количествами элементов в них. Тогда всякое размещение без повторений всех элементов S, получаемое выписыванием без повторений сначала всех элементов S₁, затем всех элементов S₂ и т.д., пока не будут выписаны без повторений все элементы множества S_k, образует перестановку элементов S. Такая перестановка отображается в исходное разбиение S₁, ... , S_k. Поэтому отображение перестановок множества S в разбиения S является сюрьективным.

Число перестановок, порождающих одно и то же разбиение множества S на части равно количеству последовательностей, составленных из перестановок элементов множеств S₁, ... , S_k, то есть определяется выражением: n₁!... n_k!.

Поскольку всего существует n! перестановок элементов A, и каждому разбиению S соответствует n₁!... n_k! таких перестановок то число различных разбиений S на части S₁, . . . , S_k равно

.

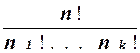Применение последней формулы к приведенному ранее примеру задачи на распределение картин по трем залам музея позволяет утверждать, что существует ровно вариантов такого распределения.