ОПРЕДЕЛЕНИЕ. Размещениями из n элементов по m элементов множества D называются m-элементные последовательности, каждый член которых является элементом D.

Размещениями из n элементов по m элементов множества D называются m-элементные последовательности, каждый член которых является элементом D.

Здесь предполагается, что m ³ 0. При этом, если m = 0, то соответствующее размещение не содержит ни одного элемента и является пустым.

Если множество D неизвестно или не уточняется, то говорят о размещениях из n по m.

Например, слово FALKON может рассматриваться как размещение из 26 элементов символов английского алфавита по 6.

Размещение называется размещением без повторений, если все входящие в него элементы являются разными.

Заметим, что для размещений с повторениями должно выполняться условие m 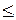n, так как в противном случае по правилу птичьих гнезд в размещении, длина которого больше числа элементов множества, из которого выбираются элементы размещения, будет повторяться хотя бы один символ.

Размещение, в котором могут встречаться одинаковые элементы, называется размещением с повторениями. Из приведенных определений следует, что всякое размещение без повторений одновременно является и размещением с повторениями.

Размещения используются для представления таких комбинаторных объектов, каждому элементу которых должно быть сопоставлено свойство, отличающее его любого из остальных элементов в составе объекта.

Определим число различных размещений из n по m без повторений. В таких размещениях первый элемент может быть выбран n способами, при всяком способе выбора первого элемента выбор второго элемента может быть осуществлен n-1разными способами и т.д. При всяком способе выбора значений первых m -1 элементов последний m-й элемент может быть выбран n - m + 1 способом.

По правилу умножения число таких размещений не зависит от множества A и равно значению произведения:

n ×(n - 1) ×... × (n - m + 1).

Для обозначения число размещений без повторений из n по m применяется специальное выражение 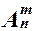. Поэтому: = .

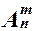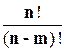В размещениях из n по m с повторениями каждый элемент такого размещения может быть выбран n способами. Поэтому по правилу умножения число размещений с повторениями из n по m равно .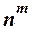

Число размещений с повторениями обозначается как 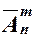. Следовательно, справедливо соотношение: = .

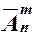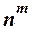Частным случаем размещений без повторений являются размещения всех элементов множества или перестановки элементов множества. Как следует из приведенных формул число P_n перестановок элементов произвольного n элементного множества равно n!