Индуктивный переход

Пусть n = k + 1. По индуктивному предположению существует ровно m₁m₂ ... m_k различных последовательностей длины k, удовлетворяющих условиям правила умножения, каждая из которых при добавлении еще одного элемента преобразуется в m_k+1 различных последовательностей длины k+1, также удовлетворяющих условиям этого правила. Поэтому общее число последовательностей длины k+1в m_k+1 раз больше числа различных последовательностей, имеющих длину k. То есть всего таких последовательностей ровно m₁ m₂ ... m_k m_k+1.

3. Правило сложения

Пусть заданы непересекающиеся конечные множества A₁, ... , A_k. Тогда мощность объединения этих множеств может быть определена по формуле:

| | = .

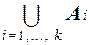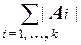Для обоснования справедливости правила сложения заметим, что в значении левой части записи правила каждый элемент объединения непересекающихся множеств A₁, . . . , A_k учтен ровно один раз. Значение в правой части правила учитывает все элементы каждого из множеств A₁, . . . , A_k. Поскольку последние множества непересекающиеся, то всякий элемент их объединения учитывается в правом значении также ровно один раз. Это означает справедливость правила сложения.

Правило умножения - основное для определения количества комбинаторных объектов. К нему сводятся различные вспомогательные комбинаторные соотношения и задачи, преобразуемые в семейства задач, решаемых с помощью этого правила.

Рассмотрим примеры задач, в которых применимо или неприменимо правило умножения.

Пример 1. Определить число различных двоичных наборов длины n, содержащих нечетное число единиц.