ОСНОВНЫЕ ПОНЯТИЯ. Комбинаторика занимается изучением свойств конечных конструкций или объектов, составленных по определенным правилам из элементов счетных множеств

ЭЛЕМЕНТЫ КОМБИНАТОРИКИ

ОСНОВНЫЕ ПОНЯТИЯ

Комбинаторика занимается изучением свойств конечных конструкций или объектов, составленных по определенным правилам из элементов счетных множеств. Такие объекты будем называть комбинаторными объектами.

Рассмотрим несколько примеров:

1) последовательности десятичных цифр, образующих правильные записи, представляющие натуральные числа. В этом случае рассматриваемые конструкции собираются в виде записей, составленных из символов десятичных цифр, в которых допускается многократное вхождение одних и тех же символов;

2) правильные записи математических выражений, составленных с помощью математических символов;

3) разнообразные комбинации цветов (букеты) также представляют собой примеры конструкций (заметим, что в данном случае правила составления букетов могут быть достаточно сложными и даже трудно объяснимыми);

4) радиоустройства, конструируемые как соединения различных радиодеталей, также можно рассматривать как комбинаторные объекты;

5) мозаики, составляемые из геометрических фигур заданной формы.

К постановкам задач изучения комбинаторных объектов приводят различные практические потребности в разнообразных областях деятельности.

Например, рассмотрим задачу нахождения вида полинома, получаемого после раскрытия скобок в выражении (x + y)^k.

Понятно, что этот полином представляет собой сумму вида: 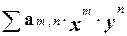Здесь a_m,n - коэффициент при произведении переменных x^myⁿ.

Для нахождения значения произвольного коэффициента a_m,n достаточно определить, сколькими разными способами в последовательности из k перемножаемых выражений (x + y) можно выделить m таких, из которых в составляемое произведение входит x. При этом из остальных m - k выражений x + y произведения (x + y)^k выбирается y.

Рассмотрим еще один пример. Пусть в продаже имеются 15видов игрушечных автомобилей, из которых составляются подарки, содержащие по три разных автомобиля.

Сколько детей может присутствовать на новогоднем празднике так, чтобы каждый ребенок получил подарок, отличный от подарков для других детей.

Нетрудно видеть, что приведенная задача равносильна задаче нахождения числа трехэлементных подмножеств множества, состоящего из 15 элементов.