ФОРМУЛА ВКЛЮЧЕНИЙ-ИСКЛЮЧЕНИЙ

Пусть A и B - произвольные множества. Тогда мощность их объединения может быть определена по формуле:

|A È B| = |A| + |B| -|A Ç B|. (1)

Если рассмотреть объединение трех множеств A, B и С, то справедлива следующая формула:

|AÈBÈС|=|A|+|B|+|С|-|AÇB|-|AÇC|-|BÇC|+|AÇBÇC|. (2)

Справедливость каждой их приведенных формул легко может быть проверена с помощью диаграмм Венна для произвольных двух и трех множеств. Для этого достаточно посчитать, сколько раз учитывается в правой и левой части каждого равенства всякий элемент объединения.

Применение приведенных формул при решении конкретных задач может быть оправдано, если нахождение каждого значения в правой части соответствующей формулы проще нахождения всего значения ее левой части.

Считается, что в общем случае объединения множеств устроены сложнее, чем пересечения множеств. Например, множество AÈBÈС в общем случае может рассматриваться как более разнородное, чем каждое из входящих в него множеств A, B и С, поскольку содержать элементы обладающие и не обладающие свойствами элементов множеств A, B и С, в разных комбинациях, в которых достаточно выполнимости лишь одного из свойств элементов этих множеств.

Действительно, в A È B È С могут содержаться элементы, обладающие только свойством элементов множества A. Там же могут содержаться элементы не из A, но обладающие свойствами элементов множеств B или C.

Множества, мощности которых используются в правых частях формул (1) и (2), образованы пересечениями отдельных множеств и поэтому более однородны, поскольку все их элементы обладают одним и тем же свойством, представляемым конъюнкцией свойств элементов множеств входящих в пересечение.

Приведенные формулы (1) и (2) могут быть обобщены на случай объединения произвольного конечного числа множеств так, чтобы свести задачу нахождения мощности объединения множеств к серии задач, связанных с нахождением мощностей нескольких пересечений множеств.

Пусть заданы конечные множества A₁ , ... , A_k и такое число i, что 0 £ i £ k. Обозначим как n_i сумму мощностей всех возможных пересечений по i таких множеств.

Заметим, что n_i является суммой 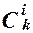слагаемых, так как существует ровно столько различных пересечений по i множеств из k.