Арифметические операции на множестве комплексных чисел

Сумма (разность) комплексных чисел есть комплексное число, определяемое равенством

= .

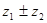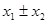
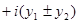Произведение двух комплексных чисел есть комплексное число, определяемое равенством

= = .

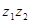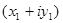
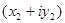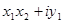
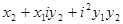Как видим, умножение комплексных чисел выполняется по правилу умножения многочленов.

Учтем, что 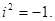и сгруппировав действительную и мнимую часть числа, получаем

= .

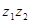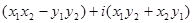Частное от деления двух комплексных чисел есть комплексное число, определяемое равенством

= .

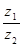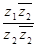Как видим, чтобы разделить комплексное число 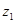на на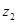до числитель и знаменатель умножить на число сопряженное делителю.

Пример 1. Даны комплексные числа 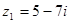и 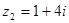. Найти , , .

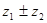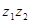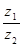Решение. = + = = .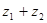

= - = = .

= = = = .

= = = = = = .

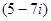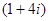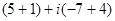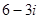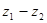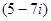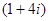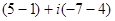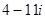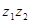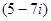
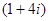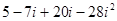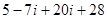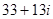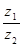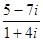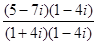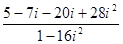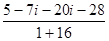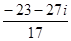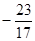
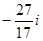Рассмотренная выше запись комплексного числа 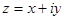называется алгебраической формой комплексного числа.