Операции над комплексными числами в тригонометрической форме.
Произведение двух комплексных чисел 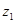 =
= 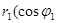
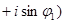 и
и 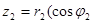
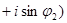 есть комплексное число, определяемое формулой
есть комплексное число, определяемое формулой 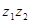 =
= 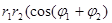
 , или
, или 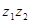 =
= 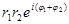 .
.
Как видим, при перемножении модули комплексных чисел умножаются, а аргументы складываются.
Частное от деления комплексного числа 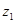 =
= 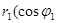
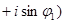 , на комплексное число
, на комплексное число 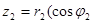
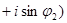 есть комплексное число, определяемое формулой
есть комплексное число, определяемое формулой 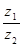 =
= 
 , или
, или 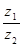 =
= 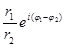 .
.
При делении модули делятся, а аргументы вычитаются.
Возведение в степень.Если 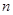 целое число, то
целое число, то 
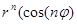
 или
или 
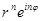 .
.
При возведении в степень комплексного числа возводится в эту степень его модуль, а аргумент умножается на показатель степени.
Извлечение корня.Если 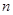 целое число, то корень из комплексного числа извлекается по формуле
целое число, то корень из комплексного числа извлекается по формуле 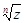 =
= 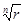
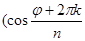
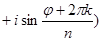 , или
, или 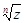 =
= 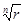
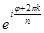 , где
, где 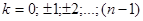 .
.
Итак, чтобы извлечь корень 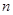 -ой степени из комплексного числа, нужно извлечь арифметический корень этой степени из модулю, а его общее значение аргумента
-ой степени из комплексного числа, нужно извлечь арифметический корень этой степени из модулю, а его общее значение аргумента 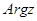
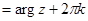
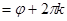 разделить на степень корня. Следовательно, извлечение корня комплексного числа – действие многозначное. Корень
разделить на степень корня. Следовательно, извлечение корня комплексного числа – действие многозначное. Корень 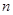 -ой степени из комплексного числа имеет
-ой степени из комплексного числа имеет 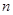 различных значений.
различных значений.
Пример 3. Найти 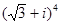 .
.
Решение.Найдем модуль и аргумент комплексного числа 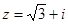 .
.
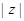 =
= 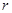 =
= 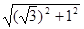 =2.
=2.
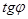 =
=  . И так как, точка
. И так как, точка 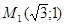 , соответствующая числу
, соответствующая числу 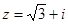 расположена в первой четверти (см. рис. 1.4), то
расположена в первой четверти (см. рис. 1.4), то 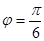 . Следовательно,
. Следовательно, 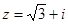 =
= 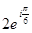 . Тогда,
. Тогда, 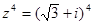 =
= 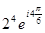 =
= 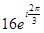 =
= 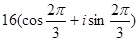 =
= 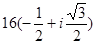 .
. 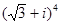 =
= 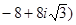 .
.

Пример 4. Дано комплексное число 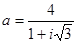 . Требуется: 1). Записать число
. Требуется: 1). Записать число 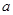 в алгебраической и тригонометрической форме. 2). Найти все корни уравнения
в алгебраической и тригонометрической форме. 2). Найти все корни уравнения 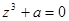 .
.
а). Запишем 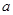 в алгебраической форме
в алгебраической форме 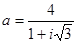 =
= 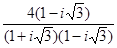 =
= 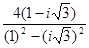 =
= 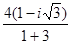 =
= 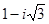 .
.
Запишем 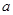 в тригонометрической форме
в тригонометрической форме 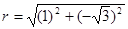 =2,
=2, 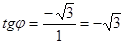 . И так как точка
. И так как точка  , соответствующая числу
, соответствующая числу 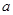 =
= 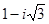 расположена в четвертой четверти (см. рис. 1.5), то
расположена в четвертой четверти (см. рис. 1.5), то 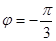 ( т.к.
( т.к. 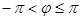 ). Следовательно,
). Следовательно, 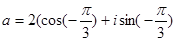 .
.
б). Решим уравнение 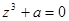 .
.  .
.
Запишем число 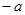 =
=  в тригонометрической форме. Модуль числа
в тригонометрической форме. Модуль числа 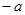 равен
равен 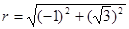 =2, а его аргумент определяем из равенства
=2, а его аргумент определяем из равенства 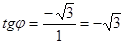 и так как точка
и так как точка 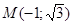 , соответствующая числу
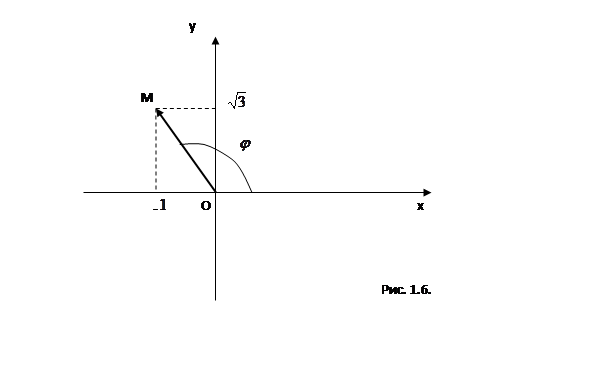
, соответствующая числу 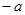 расположена в третьей четверти (см. рис. 1.6), то
расположена в третьей четверти (см. рис. 1.6), то 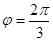 ( т.к.
( т.к. 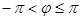 ). Следовательно, в тригонометрической форме
). Следовательно, в тригонометрической форме  . Поэтому
. Поэтому  =
= 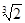
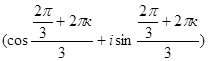 , где
, где 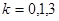 .
.

При 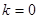
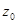 =
= 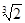
 =
= 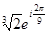 .
.
При 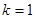
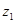 =
= 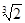
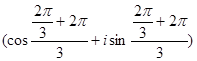 =
= 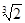
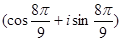 =
= 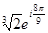 .
.
При 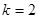
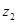 =
= 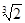
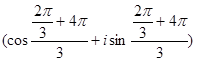 =
= 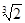
 =
= 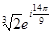 .
.
Дата добавления: 2015-10-09; просмотров: 1333;
