Понятие комплексного числа
Лекция 1. КОМПЛЕКСНЫЕ ЧИСЛА.
Комплексным числом называется выражение
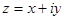 ,
,
где  , а символ и называется мнимой единицей и определяется равенством
, а символ и называется мнимой единицей и определяется равенством 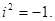 При этом,
При этом,  называется действительной частью комплексного числа и обозначается
называется действительной частью комплексного числа и обозначается
 ,
,
а 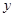 - мнимой частью и обозначается
- мнимой частью и обозначается
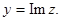
Геометрически в декартовой системе координат число 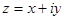 можно изобразить точкой
можно изобразить точкой 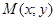 . Абсцисса и ордината точки
. Абсцисса и ордината точки 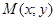 соответственно равны действительной и мнимой частям комплексного числа. Например, комплексному числу
соответственно равны действительной и мнимой частям комплексного числа. Например, комплексному числу 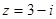 соответствует точка
соответствует точка 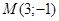 (рис.1 1).
(рис.1 1).
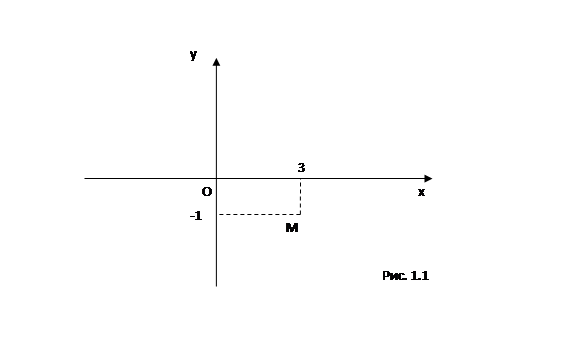
В общем случае между точкой 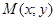 и комплексным числом
и комплексным числом 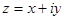 существует взаимно однозначное соответствие.
существует взаимно однозначное соответствие.
Если 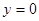 имеем действительное число
имеем действительное число  , которому соответствует точка
, которому соответствует точка 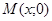 на оси
на оси 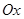 . Ось
. Ось 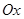 называется действительной осью. Таким образом, действительные числа есть частный случай комплексных чисел.
называется действительной осью. Таким образом, действительные числа есть частный случай комплексных чисел.
Если 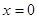 имеем чисто мнимое число
имеем чисто мнимое число 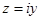 , которому соответствует точка
, которому соответствует точка  на оси
на оси 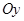 . Ось
. Ось 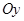 называется мнимой осью.
называется мнимой осью.
Числа 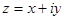 и
и  называются комплексно-сопряженными или просто сопряженными. Они отличаются друг от друга, только знаком мнимой части.
называются комплексно-сопряженными или просто сопряженными. Они отличаются друг от друга, только знаком мнимой части.
Два комплексных числа 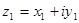 и
и 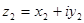 называются равными, если равны их действительные и мнимые части, т. е.
называются равными, если равны их действительные и мнимые части, т. е.

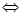

В частности 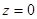 , если
, если 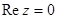 и
и 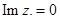 .
.
Дата добавления: 2015-10-09; просмотров: 804;
