Тригонометрическая и показательная формы комплексного числа

Задано комплексное число 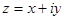. На комплексной плоскости ему соответствует точка 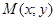. С каждой точкой 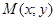связан радиус-вектор этой точки 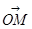(рис 1.2).

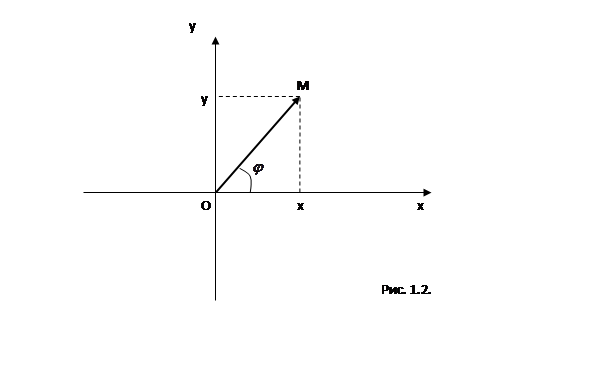
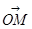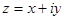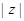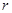Длина радиус вектора называется модулем комплексного числа и обозначается или . Из чертежа (рис. 1.2) видно, что

= = .

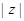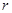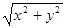Угол 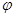, образованный радиус-вектором 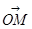с положительным направлением оси 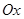, называется аргументом комплексного числа 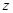и обозначается 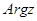. Из значений 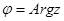выделяется главное значение 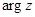, удовлетворяющее условию . 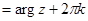, где .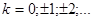

Следует помнить, что , если 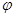отсчитывается от положительного направления оси 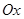против хода часовой стрелки, и 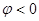при противоположном отсчете.

Из чертежа (рис. 1.2) видно, что

, .

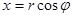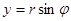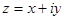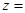
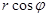
Следовательно, комплексное число можно представить как 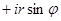, или

.

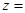
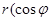
Эту запись называют тригонометрической формойкомплексного числа.

Связь между тригонометрическими и показательными функциями выражается формулой Эйлера

.

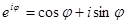Отсюда следует показательная форма записи комплексного числа

.

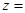
Пример 2. Даны комплексные числа 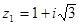и . Представить их в тригонометрической и показательной форме.

Возьмем первое число ,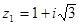

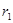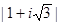= = =2,

= = .

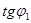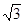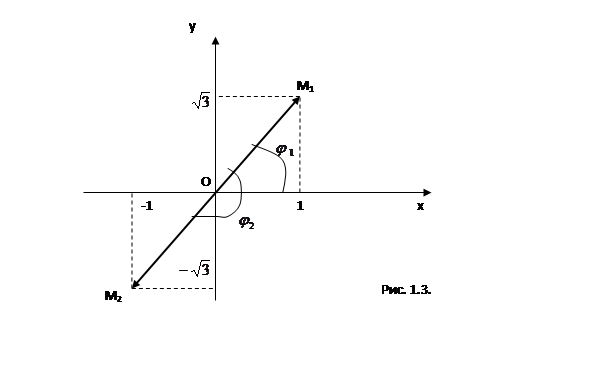
Так как, точка , соответствующая числу 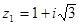расположена в первой четверти (см. рис. 1.3), то 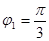. Тогда тригонометрическая форма числа 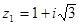будет 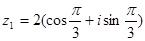, а показательная - .

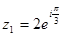Для второго числа , 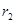= = 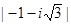=2, = = 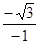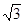. И так как, точка 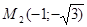, соответствующая числу расположена в третьей четверти (см. рис. 1.3), то 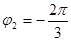(т.к. ).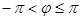

Тогда тригонометрическая форма числа будет , а показательная - .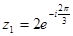

Операции умножения, деления, возведения в степень и извлечение корня удобнее производить над комплексными числами не в алгебраической, а в тригонометрической и показательной форме.