Упражнения для самостоятельной работы. 1. Постройте на координатной прямой и запишите промежутками множества A и B, используя геометрический смысл модуля разности двух действительных чисел:
1. Постройте на координатной прямой и запишите промежутками множества A и B, используя геометрический смысл модуля разности двух действительных чисел:
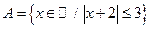 и
и 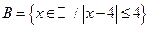 .
.
Запишите 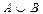 ,
, 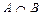 ,
, 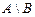 ,
, 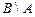 ,
, 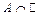 ,
, 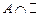 ,
, 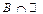 ,
, 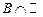 .
.
2. Запишите элементы следующих множеств:
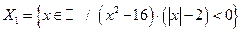 ;
; 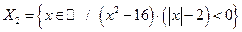 ;
;
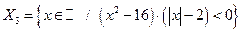 .
.
3. Запишите элементы следующих множеств:
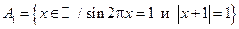 ;
; 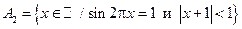 ;
;
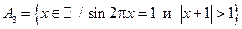 .
.
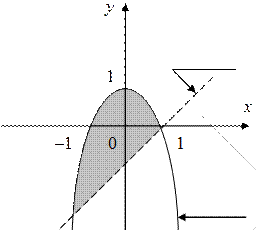
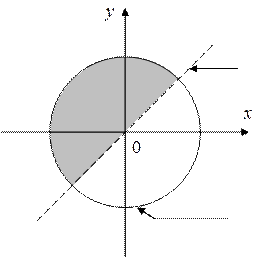
4. Постройте каждое из следующих множеств точек на координатной плоскости XOY:
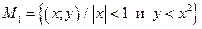 ;
; 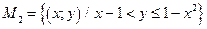 ;
;
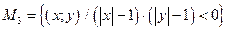 ;
; 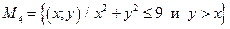 .
.
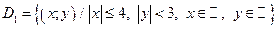 ;
;
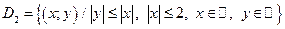 .
.
5. Известно описание множеств X и Y:
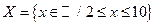 ,
, 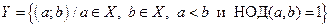 .
.
Перечислите все элементы множества Y и укажите их количество.
Ответы к упражнениям для самостоятельной работы
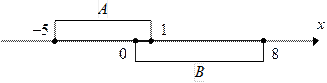
1. 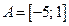 ; ; 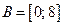 ; ;
| 
|
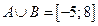 ; ; 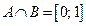 ; ; 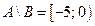 ; ; 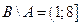 ; ;
| 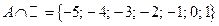 ; ; 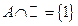 ; ; 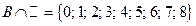 ; ; 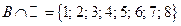 . .
|
2. 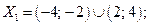
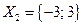 ;
; 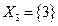 .
.
3. 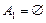 ,
, 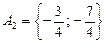 ,
, 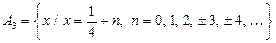 .
.
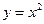 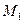 4. 4. 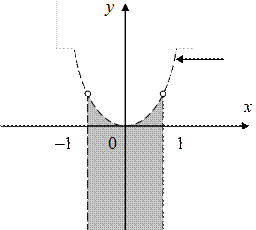
| 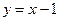 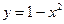    
| ||||
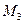     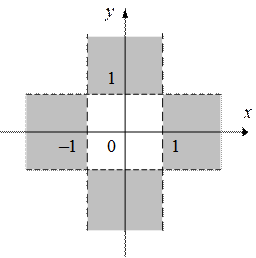
| 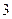 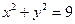 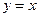    
| ||||
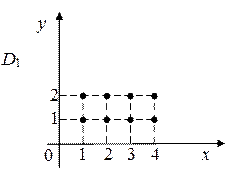
|
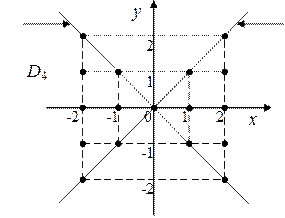
| ||||
5. 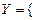 (2; 3), (2; 5), (2; 7), (2; 9), (3; 4), (3; 5), (3; 7), (3; 8), (3; 10), (4; 5), (4; 7), (4; 9),
(5; 6), (5; 7), (5; 8), (5; 9), (6; 7), (7; 8), (7; 9), (7; 10), (8; 9), (9; 10) }
Количество элеменетов в множестве Y равно 22. (2; 3), (2; 5), (2; 7), (2; 9), (3; 4), (3; 5), (3; 7), (3; 8), (3; 10), (4; 5), (4; 7), (4; 9),
(5; 6), (5; 7), (5; 8), (5; 9), (6; 7), (7; 8), (7; 9), (7; 10), (8; 9), (9; 10) }
Количество элеменетов в множестве Y равно 22.
|
Вопросы для самопроверки
Что называется множеством действительных чисел?
Что называется суммой двух действительных чисел?
Что такое свойство коммутативности операции сложения?
Что такое свойство ассоциативности операции сложения?
Что такое нейтральный элемент операции сложения?
Что такое разностью чисел a и b?
Что называется произведением двух действительных чисел?
Что такое свойство коммутативности операции умножения?
Что такое свойство ассоциативности операции умножения?
Что такое нейтральный элемент операции умножения?
Что называется частным от деления числа a на число b?
Что такое свойство дистрибутивности произведения относительно суммы?
Что такое упорядоченность множества действительных чисел?
Что такое отношение порядка?
Что такое свойство плотности множества действительных чисел?
Что называется неравенствами или сравнениями действительных чисел?
Что такое непрерывность множества действительных чисел?
Что такое множество натуральных чисел?
Что такое множество целых чисел?
Что такое множество рациональных чисел?
Что такое множество иррациональных чисел?
Что такое универсальное числовое множество?
Что такое простые числа?
Что такое составные числа?
Что такое взаимно простые числа?
Что такое наименьшее общее кратное (НОК) ?
Что такое наибольший общий делитель (НОД)?
Что называется дискретным множеством?
Что называется непрерывным множеством?
Глоссарий
взаимно простые числа это…(стр. 22)
дискретным множеством называется…(стр. 24)
множество иррациональных чисел это…(стр. 21)
множество натуральных чисел это…(стр. 21)
множество рациональных чисел это…(стр. 21)
множество целых чисел это…(стр. 21)
множеством действительных чисел называется…(стр. 18)
наибольший общий делитель (НОД) это…(стр. 22)
наименьшее общее кратное (НОК) это…(стр. 22)
нейтральный элемент операции сложения это…(стр. 18)
нейтральный элемент операции умножения это…(стр. 19)
непрерывность множества действительных чисел это…(стр. 20)
непрерывным множеством называется…(стр. 24)
неравенствами или сравнениями действительных чисел называется…(стр. 19)
отношение порядка это…(стр. 19)
произведением двух действительных чисел называется…(стр. 19)
простые числа это…(стр. 22)
разностью чисел a и b называется…(стр. 18)
свойство ассоциативности операции сложения это…(стр. 18)
свойство ассоциативности операции умножения это…(стр. 19)
свойство дистрибутивности произведения относительно суммы это…(стр. 19)
свойство коммутативности операции сложения это…(стр. 18)
свойство коммутативности операции умножения это…(стр. 19)
свойство плотности множества действительных чисел это…(стр. 19)
составные числа это…(стр. 22)
суммой двух действительных чисел называется…(стр. 18)
универсальное числовое множество это…(стр. 21)
упорядоченность множества действительных чисел это…(стр. 19)
частным от деления числа a на число b называется…(стр. 19)
Дата добавления: 2015-10-19; просмотров: 1608;
