Окрестности точек числовой прямой
Окрестностью конечной точки 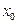 числовой прямой называется любой интервал, содержащий точку
числовой прямой называется любой интервал, содержащий точку 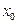 , (рис. 18);
, (рис. 18);
обозначение окрестности точки 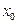 :
: 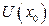 .
.
В частности, симметричный относительно точки 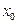 интервал
интервал 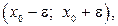
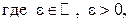 называется e-окрестностью конечной точки
называется e-окрестностью конечной точки 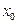 , (рис. 18); обозначение e-окрестности точки
, (рис. 18); обозначение e-окрестности точки 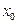 :
: 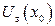 ;
;
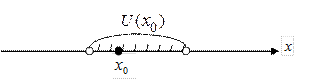
e-окрестность точки х0 можно описать как множество следующим образом:
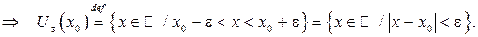
| 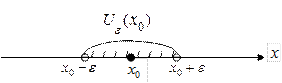
|
| Рис. 18 |
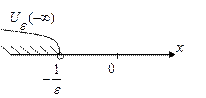
Определения e-окрестностей бесконечно удаленных точек:
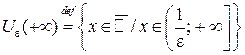
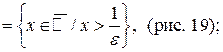
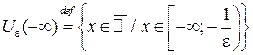
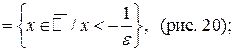
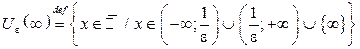
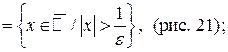
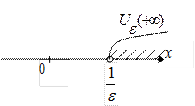
| 
|
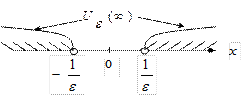
|
| Рис. 19 | Рис. 20 | Рис. 21 |
Пример (e-окрестности точек 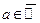 )
)
Запишем e-окрестности некоторых точек, положив e = 1 и e = 0,1:
| если e = 1, то | 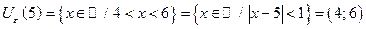 , , 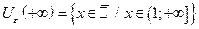 , , 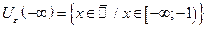 , , 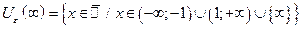 ; ;
|
| если e = 0,1, то | 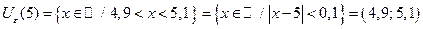 , , 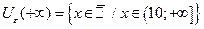 , , 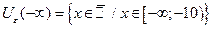 , , 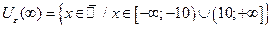 . .
|
Дата добавления: 2015-10-19; просмотров: 2512;
