Основные свойства окрестностей
Нетрудно проверить, что являются справедливыми перечисленные ниже свойства окрестностей.
1. Свойство о существовании непересекающихся окрестностей
У любых двух различных точек расширенной числовой прямой всегда существуют непересекающиеся окрестности (рис. 22).
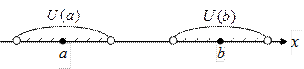
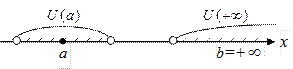
Рис. 22
Так как окрестность каждой точки можно «измерить» (описать) числом  , то рассматриваемое свойство для
, то рассматриваемое свойство для  -окрестностей записывается так:
-окрестностей записывается так:
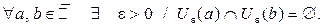
2. Свойство о пересечении двух окрестностей
Пересечение двух окрестностей одной и той же точки (конечной или бесконечно удаленной) является также окрестностью этой точки,
(рис. 23).

| 
|
| Рис.23 |
3. Свойство о сужении e-окрестностей
e-окрестность любой точки 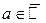 сужается, если уменьшать число e >0.
сужается, если уменьшать число e >0.
4. Понятие о проколотых окрестностях
Проколотой окрестностью точки 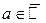 называется любая окрестность этой точки, которая не включает в себя саму точку a.
называется любая окрестность этой точки, которая не включает в себя саму точку a.
Обозначения проколотых окрестностей: 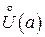 или
или 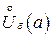 .
.
Проколотая e-окрестность конечной точки a описывается и изображается так, как показано на рис. 24.
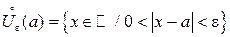
| 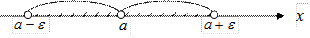
|
| Рис. 24 |
Примеры (проколотые e-окрестности точек  )
)
1) a = 3, e = 0,1 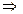 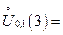  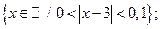
|
2)  , e=0,1 , e=0,1 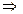 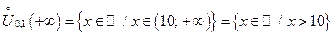 ; ;
|
3) 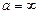 , e = 0,1 , e = 0,1  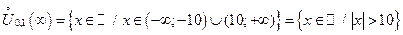 . .
|
Дата добавления: 2015-10-19; просмотров: 5267;
