ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМОЙ, ТОЧКИ И ПЛОСКОСТИ

Прямая принадлежит плоскости, если она имеет с плоскостью две общие точки. На рис. 217 проекции прямой АЕ проходят через проекции а' и а — проекции вершины А треугольника ABC и проекции e и e' — проекции точки пересечения прямой АЕ со стороной ВС треугольника ABC. Прямая АЕ имеет с треугольником ABC две общие точки: А и Е, следовательно, прямая АЕ принадлежит плоскости, которая задана треугольником ABC.

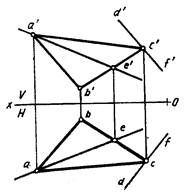
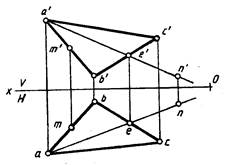
Рис. 217 Рис. 218

Прямая принадлежит плоскости, если она проходит через точку, принадлежащую плоскости, и параллельна прямой, лежащей в этой плоскости. Проекции прямой DF (d'f, df) (рис. 217) параллельны проекциям стороны АВ треугольника ABC (f'd'║a'b' и fd║ab) и проходят через одноименные проекции точки С (с и с'), принадлежащей треугольнику ABC. Следовательно, прямая FD принадлежит плоскости, которая задана треугольником ABC, так как она проходит через точку, принадлежащую треугольнику, и параллельна одной из его сторон.

Точка принадлежит плоскости, если она принадлежит прямой, лежащей в этой плоскости. Точка М (рис. 218) принадлежит плоскости, которая задана треугольником ABC, так как ее проекции m и m' лежат на одноименных проекциях отрезка АВ (ab и а'b'), который является стороной треугольника ABC. Точка N также принадлежит плоскости треугольника AВС, так как фронтальная проекция n' точки N лежит на продолжении фронтальной проекции прямой АЕ (а'е'), а горизонтальная проекция n точки N лежит на продолжении горизонтальной проекции прямой АЕ (ае), и обе проекции лежат на одной линии связи.

Прямая параллельна плоскости, если она параллельна прямой, лежащей в этой плоскости. Если плоскость задана треугольником ABC, то, чтобы провести через точку D прямую DE параллельно данной плоскости (рис. 219), нужно провести ее проекции параллельно одноименным проекциям одной из сторон треугольника ABC. На рис. 219 de║bc и d'e'║b'c'.

Следовательно, DE║BC. На рис. 220 построены проекции прямой NM и плоскости, заданной треугольником ABC. Необходимо проверить, параллельна ли прямая MN плоскости треугольника ABC. Попробуем построить через вершину А треугольника ABC прямую АЕ, параллельную MN. Для этого проводят горизонтальную проекцию ае прямой АЕ параллельно mn и строят фронтальную проекцию а'е'. Если прямая NM параллельна плоскости треугольника ABC, то построенная фронтальная проекция a'e' должна быть параллельна m'n'. Так как а'е' на рис.220 не параллельна m'n', прямая MN не параллельна плоскости треугольника ABC.

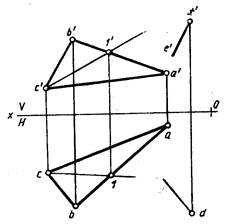
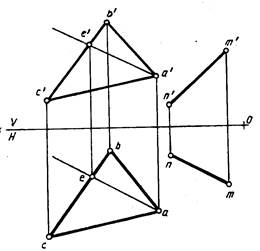
Рис. 219 Рис. 220

С помощью рассмотренных выше положений решается ряд задач на построение. Рассмотрим некоторые из них.

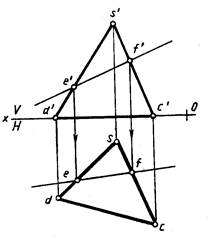
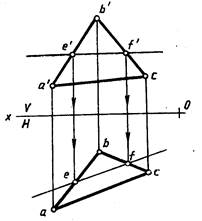
Рис. 221 Рис. 222

Задача 1. В плоскости треугольника DSC провести прямую EF. Чтобы прямая EF принадлежала плоскости треугольника АВС, достаточно, чтобы две ее точки лежали в плоскости треугольника. Проводят произвольно фронтальную проекцию e'f' прямой EF (рис. 221) так, чтобы она пересекала фронтальные проекции двух сторон треугольника ABC а точках е' и f'. Горизонтальные проекции е и f точек Е и F строят с помощью линий проекционной связи. Из точек е' и f' проводят линии проекционной связи до пересечения с соответствующими горизонтальными проекциями сторон треугольника AВС.

Если в плоскости треугольника AВС нужно провести горизонталь, то фронтальную проекцию горизонтали проводят параллельно оси Ох (рис. 222).

Задача 2. Задана фронтальная проекция k' точки К, лежащей в плоскости треугольника DSC, требуется построить ее горизонтальную проекцию. Для этого проводят фронтальную проекцию горизонтали e'k' через заданную фронтальную проекцию k' точки К и строят горизонтальную проекцию горизонтали, опустив из точки е' линию связи до пересечения со стороной sd и проведя из точки е прямую параллельно стороне dc, так как dc является горизонтальным следом плоскости треугольника DSC. Опустив из точки k' линию связи до пересечения с прямой, параллельной dc, получают горизонтальную проекцию k точки К. Точка будет лежать в плоскости, так как она лежит на горизонтали этой плоскости (рис. 223, а).

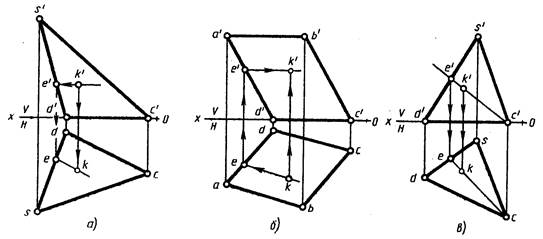
Рис. 223

На рис. 223, б показано построение фронтальной проекции k' точки К', принадлежащей плоскости параллелограмма ABCD, по заданной горизонтальной проекции k. Сторона dc является горизонтальным следом плоскости. Известно, что все горизонтали плоскости параллельны горизонтальному следу этой плоскости. Поэтому горизонтальная проекция ek горизонтали проведена через точку k параллельно dc. Фронтальная проекция k' точки К находится на фронтальной проекции горизонтали, параллельной оси Ох.

На рис 223,в показано построение горизонтальной проекции k точки К с помощью вспомогательной прямой, проходящей через вершину треугольника DSC — точку С. Через заданную фронтальную проекцию k' точки К и точку с' проводят фронтальную проекцию вспомогательной прямой, которая пересечет сторону d's' фронтальной проекции треугольника DSC в точке е'. Из точки е' проводят линию проекционной связи, находят горизонтальную проекцию е точки Е, проводят горизонтальную проекцию се вспомогательной прямой СЕ и на ней, опустив из точки k' линию связи, находят горизонтальную проекцию k точки К. Фронтальную проекцию вспомогательной прямой можно было провести через любую фронтальную проекцию вершины треугольника ABC.