Разбиение множества на подмножества
Говорят, что множество А разбито на подмножества 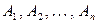 , если выполняются следующие два условия:
, если выполняются следующие два условия:
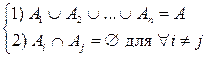 то есть объединение подмножеств
то есть объединение подмножеств 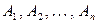 совпадает с множеством A и никакие два из этих подмножеств не пересекаются, (рис. 9). совпадает с множеством A и никакие два из этих подмножеств не пересекаются, (рис. 9).
| 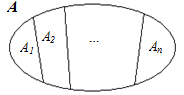 Рис. 9
Рис. 9
|
Основные свойства операций над множествами
Являются очевидными или нетрудно доказываются, например, с помощью диаграмм Эйлера-Венна, ниже перечисленные свойства операций над множествами.
I. Коммутативность операций (переместительное свойство):
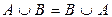 (коммутативность объединения);
(коммутативность объединения);
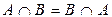 (коммутативность пересечения);
(коммутативность пересечения);
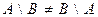 (некоммутативность разности);
(некоммутативность разности);
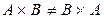 (некоммутативность декартова произведения).
(некоммутативность декартова произведения).
II. Ассоциативность операций (сочетательное свойство):
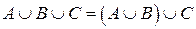 (ассоциативность объединения);
(ассоциативность объединения);
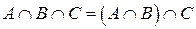 (ассоциативность пересечения).
(ассоциативность пересечения).
III. Дистрибутивность операций (распределительное свойство):
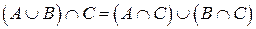 (дистриб. пересечения относительно
(дистриб. пересечения относительно
объединения);
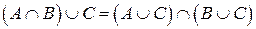 (дистриб. объединения относительно
(дистриб. объединения относительно
пересечения).
IV. Особые случаи результатов операций над множествами:
если 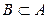 , то
, то 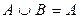 ,
, 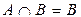 ;
;
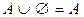 ,
, 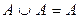 ,
, 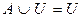 ;
;
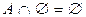 ,
, 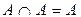 ,
, 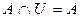 ;
; 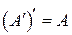 .
.
V. Законы двойственности:
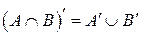 ;
; 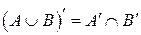 .
.
Дата добавления: 2015-10-19; просмотров: 1905;
