Основные операции над множествами. К основным операциям над множествами относятся объединение, пересечение, разность, дополнение, декартово произведение

К основным операциям над множествами относятся объединение, пересечение, разность, дополнение, декартово произведение, разбиение множества на подмножества.

1. Объединением множеств А и В называется множество, состоящее из таких и только таких элементов, которые принадлежат хотя бы одному из множеств A или B, (рис. 4).

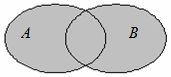Рис. 4

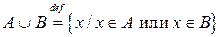Определение объединения множеств.

Для набора множеств 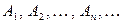операция объединения определяется так:

.

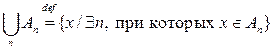2. Пересечением множеств А и Вназывается множество, состоящее из таких и только таких элементов, которые принадлежат обоим множествам A и B, (рис. 5).

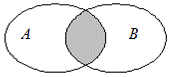Рис. 5

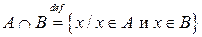Определение пересечения множеств.

Для набора множеств 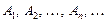операция пересечения определяется так:

.

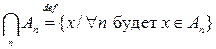3. Разностью множества А и множества Вназывается множество, состоящее из таких и только таких элементов, которые принадлежат множеству A и не принадлежат множеству B, (рис. 6).

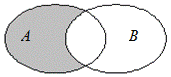
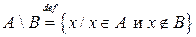	Определение разности множеств;
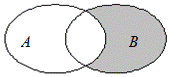Рис. 6	.

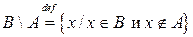4. Если 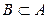, то разность 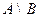называется дополнением к множеству B в множестве А, (рис. 7).

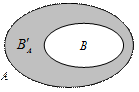Рис. 7

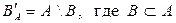Определение дополнения к множеству

Замечание (о дополнении в универсальном множестве)

Для нескольких рассматриваемых множеств, состоящих из элементов одной природы, можно ввести так называемое универсальное множество, для которого все рассматриваемые множества являются подмножествами. Например, для числовых множеств универсальным можно считать множество действительных чисел .

Универсальное множество обычно обозначается буквой 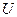и на диаграмме Эйлера-Венна изображается прямоугольником. Дополнение к некоторому множеству 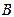в универсальном множестве 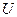обозначается только штрихом, (рис. 8).

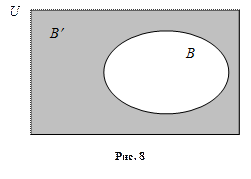
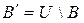, где U - универсальное множество

5. Декартово произведение множества А на множество В
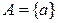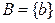Если и , то ,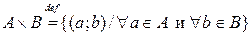
то есть декартово (или прямое) произведение множества A на множество B состоит из всех возможных упорядоченных пар, у которых первый элемент взят из множества A, а второй – из множества B.