Упражнения для самостоятельной работы

1. Дано, что .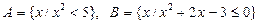
Запишите промежутками и постройте геометрически на координатной прямой множества А, B, 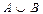, , 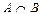, 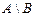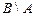. Опишите и постройте на координатной плоскости множества 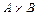и .

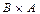2. Дано, что .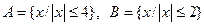
Запишите и постройте геометрически на координатной прямой множества А, B, .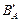

3. Определите элементы следующих множеств:
, ,
, ,
, .

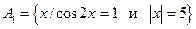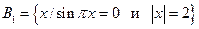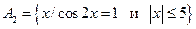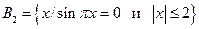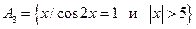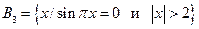4. Постройте множества точек на координатной плоскости XOY:
, .

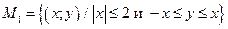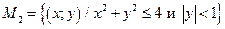5. Дано множество .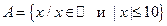

Составьте разбиение множества А на подмножества по признаку делимости его элементов на числа 2 и 5.

6. Дано: множество ;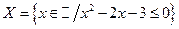

условие (1): х – неположительное число, большее чем -0.5;

условие (2): х – удовлетворяет неравенству .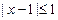

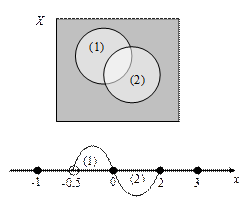
Составьте разбиение множества Х на подмножества по признаку удовлетворения его элементов условиям (1) и (2). Сделайте иллюстрацию к разбиению с помощью диаграммы Эйлера-Венна и на координатной прямой.

Ответы к упражнениям для самостоятельной работы

1. ; ; ; ; ; ;
;	.
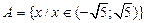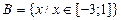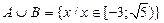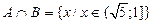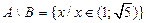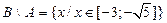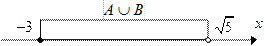
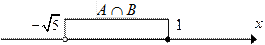
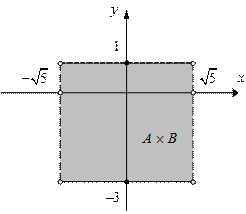
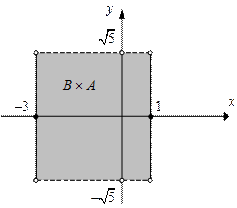
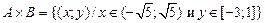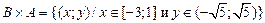2. .
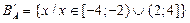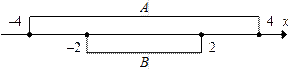
3. , ; , ; , .
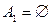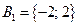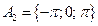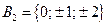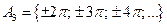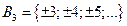4.
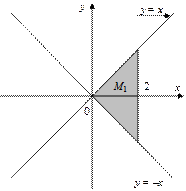
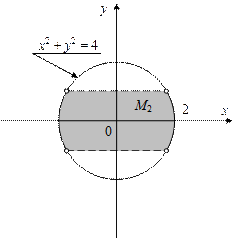
5. , , , .
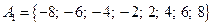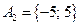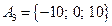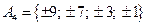6.		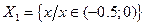- множество х, удовлетворяющих условию (1) и не удовлетворяющих условию (2);
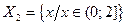
		- множество х, удовлетворяющих условию (2) и не удовлетворяющих условию (1);
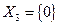
		- множество х, удовлетворяющих обоим условиям (1) и (2);
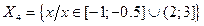
		- множество х, не удовлетворяющих ни условию (1), ни условию (2).

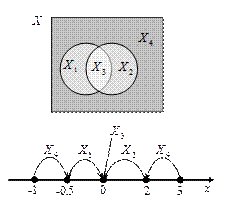
Вопросы для самопроверки

Что такое множество?

Что такое конечное множество?

Что такое бесконечное множество?

Что такое числовое множество?

Что называется равными множествами?

Что называется подмножеством?

Что называется кругами Эйлера, или диаграммами Эйлера-Венна?

Что называется подмножеством?

Что называется объединением множеств А и В?

Что называется пересечением множеств А и В?

Что называется разностью множества А и множества В?

Что называется дополнением к множеству B в множестве А?

Что такое универсальное множество?

Что такое декартово произведение множества А на множество В?

Что такое разбиение множества на подмножества?

Что такое коммутативность операций?

Что такое ассоциативность операций?

Что такое дистрибутивность операций?

Что такое особые случаи результатов операций над множествами?

Что такое законы двойственности?

Глоссарий

ассоциативность операций это…(стр. 10)

бесконечное множество это…(стр. 5)

декартово произведение множества А на множество В это…(стр. 9)

дистрибутивность операций это…(стр. 10)

дополнением к множеству B в множестве называется…(стр. 8)

законы двойственности это…(стр. 10)

коммутативность операций это…(стр. 10)

конечное множество это…(стр. 5)

кругами Эйлера, или диаграммами Эйлера-Венна называется…(стр. 6)

множество это…(стр. 5)

объединением множеств А и В называется…(стр. 7)

особые случаи результатов операций над множествами это…(стр. 10)

пересечением множеств А и В называется…(стр. 8)

подмножеством называется…(стр. 6)

подмножеством называется…(стр. 7)

равными множествами называется…(стр. 6)

разбиение множества на подмножества это…(стр. 9)

разностью множества А и множества В называется…(стр. 8)

универсальное множество это…(стр. 8)

числовое множество это…(стр. 5)

§ 2. Множество действительных чисел: определение, геометрическая интерпретация, модуль, стандартные подмножества

Содержание

2.1. Аксиоматическое определение множества действительных чисел. 18

2.2. Модуль действительного числа. 20

2.3. Стандартные подмножества множества действительных чисел ... 21

2.4. Примеры работы на множестве ... 23

2.5. Дискретные и непрерывные множества. 24

2.6. Упражнения для самостоятельной работы.. 25

Вопросы для самопроверки.. 27

Глоссарий 27