Способы задания множеств. Множество — это совокупность объектов или явлений, объединенных по какому-нибудь общему для них признаку
Множество — это совокупность объектов или явлений, объединенных по какому-нибудь общему для них признаку. Множество состоит из элементов. Множество считается заданным, если о каждом элементе можно однозначно сделать вывод о том, входит или не входит этот элемент в рассматриваемое множество.
Если количество элементов множества может быть выражено некоторым натуральным числом или нулем, то имеем конечное множество. Количество элементов в конечном множестве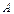 
обозначается 
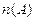. Пустое множество 
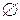считается конечным и 
.
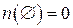Если количество элементов множества не может быть выражено натуральным числом или нулем, то имеем бесконечное множество.
Если элементами множества являются числа, то имеем числовое множество.
Основные способы описания множества
1) 
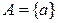— множество состоит из элементов a;
2) 
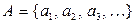— множество задано списком своих элементов;
3) 
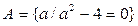— множество задано характеристическим свойством своих элементов.
Примеры (задание множеств)
¥ = {1, 2, 3, 4, 5, ¼} – множество натуральных чисел;
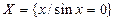– множество корней уравнения 
;
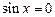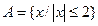– множество решений неравенства 
;
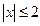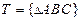– множество треугольников с вершинами в точках А, В, С;
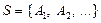– множество исходов, связанных с некоторым экспериментом.
Если множества состоят из одних и тех же элементов, то они называются равными множествами.
Например, 1)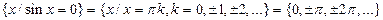 
;
2) 
.
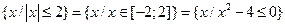Дата добавления: 2015-10-19; просмотров: 1082;