ПОЛЯ. ГРАДИЕНТ ПОТЕНЦИАЛА.
Для понимания свойств электрического поля большое значение имеет понятие разности потенциалов или электрического напряжения.К этому понятию мы придем, рассматривая работу сил электрического поля.
Предположим, что электрический заряд qперемещается в каком -либо электрическом поле (например, в электрическом поле плоского конденсатора, рис. 12), из некоторой точки 1 в другую точку 2. Так как на заряд в электрическом поле действует сила, то при таком перемещении будет произведена определённая работа А12. Ясно, что если тот же заряд перемещается по прежнему пути в обратном направлении (от точки 2 к точке 1), то величина работы будет та же самая, но изменится её знак, т.е. А12 = -А21.
Покажем, что работа по перемещению заряда в электрическом поле не зависит от формы пути, по которому движется заряд, и определяется только положением точек 1 и 2 - начала и конца пути заряда.
Допустим, что это не так, и что работа А(L)12 при перемещении заряда вдоль контура L (рис.12) не равна работе А (L’) 12 для контура L’, причём оба контура соединяют одни и те же точки 1 и 2.
 |  |
 + -
+ -

 + 2 -
+ 2 -

 +1
+1
 + -
+ -
L L¢
 + -
+ -
 + -
+ -
Рис. 12.
Тогда перемещая заряд по замкнутому контуру, составленному из контуров L и L’, мы найдём, что электрические силы совершают работу
А(L)12 + А(L’)21= А(L)12- А(L’)12,
которая не равна нулю. Но это противоречит общему закону сохранения энергии. Если заряды, создающие электрическое поле, неподвижны, то при перемещении подвижного заряда в окружающих телах не происходит никаких процессов. После возвращения заряда в исходную точку 1 мы не имеем никаких изменений в рассматриваемой системе тел и поэтому не можем получить ни выигрыша работы, ни её потери. Это значит, что наше предположение неверно, и что в действительности
А(L)12 =А(L’)12
Т.о., в электростатическом поле работа перемещении заряда между двумя точками не зависит от формы пути, соединяющего эти точки.Иными словами: при перемещении заряда в электростатическом поле по замкнутому контуру работа равна нулю.

Если заряд q0 перемещается в поле,создаваемом_системой точечных зарядов q1,q2,...qn , то на него действует сила
 ``
`` 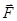 =
= 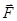 1 +
1 + 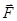 2 +….+
2 +….+ 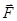 n,
n, 
а работа А равнодействующей силы равна алгебраической сумме работ составляющих сил
А=А1+А2 + Аз+...+ Аn.
Полная работа А, как и каждая из работ А1 , А2,.. Аn зависит от начального и конечного положений заряда q, но не зависит от формы его пути. _
Работа, совершаемая силой `F при перемещении заряда q0 на отрезке d,

где 

-угол между направлениями векторов `Е и dl.
В случае конечного перемещения заряда q0 източки а в точкув работа сил поля

Работа, которую совершают силы электрического поля, перемещая единичный положительный заряд по замкнутому пути L , численно равна

Этот интеграл называется циркуляцией напряженностивдоль замкнутого контура L.
 |
Поскольку работа при перемещении заряда по любому замкнутому контуру равна нулю, то
Т.е. циркуляция напряженности электростатического поля вдоль замкнутого контура равна нулю.Силовое поле, напряжённость Е которого удовлетворяет такому условию, называется потенциальным полем.Т.о. электростатическое поле является потенциальным.
РАЗНОСТЬ ПОТЕНЦИАЛОВ.Если в электрическом поле перемещается заряд (+1), то работа зависит только от существующего электрического поля и поэтому может служить его характеристикой. Она называется разностью потенциаловточек 1 и 2 в данном электрическом поле или электрическим напряжениеммежду точками 1 и 2.
 |
Разность потенциалов двух точек 1 и 2 в электростатическом поле измеряется работой, совершаемой силами поля при перемещении заряда (+1) из точки 1 в 2, т.е.
(1)
Еl - проекция вектора Е на направление dl. Интегрирование производится вдоль любого контура L, соединяющего рассматриваемые точки, в направлении от точки 1 к точке 2.
Если в электрическом поле перемещается не единичный заряд, а заряд произвольной величины q, то в каждой точке сила, действующая на заряд, увеличится в q раз. Поэтому работа А12, совершаемая силами поля при перемещении q из 1 в 2,равна
А12 =qU12. (2)
Из сказанного следует, что физический смысл имеет только разность потенциаловили напряжение между двумя точками поля, т.к. работа определена только тогда, когда заданы две точки - начало и конец пути. Несмотря на это, часто говорят просто о потенциале или напряжении в данной точке. Однако при этом всегда имеют в виду разность потенциалов, но подразумевают, что одна из точек выбрана заранее. Такую постоянную точку часто выбирают "в бесконечности", т.е. на достаточном удалении от всех заряженных тел.
Если заряд (+1) перемещается по замкнутому контуру, например, сначала из 1 в 2 по контуру L (рис.12), а затем от 2 к 1 вдоль L’, то
U12 +U21 =U12 -U12 =0 (3)
Дата добавления: 2015-10-19; просмотров: 1283;
