Пример 1. Равномерно-заряженная плоскость.

Имеется безграничная плоскость, заряженная равномерно с поверхностной плот­ностью заряда s. Найти напряженность Е(х), где х - расстояние до плоскости.

Из симметрии задачи очевидно, что линии напряженности должны быть направлены симметрично в обе стороны от плоскости ^ ей. В этом случае в качестве замкнутой поверхности в теореме Остроградского-Гаусса удобно выбрать прямой цилиндр, перпендикулярный к заряженной плоскости, ограниченный двумя плоскими основаниями, перпендикулярными к силовым линиям и расположенными по обе стороны заряженной плоскости (рис.7).

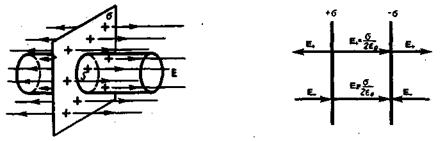
Рис. 7. Рис.8.

Т.к. образующие цилиндра параллельны вектору напряженности электрического поля `Е, то поток через боковую поверхность цилиндра равен нулю и поэтому полный по­ток сквозь цилиндр равен сумме потоков через его основания

Ф =^:2ЕS.

Полный заряд, заключенный внутри цилиндра равен Ss. Поэтому применяя теорему О-Г, имеем:

2ЕS =sS/e₀, откуда

Е = s/2e₀,

т.е. `Е не есть функция расстояния. Следовательно `Е = соnst по величине и по направлению.

Если плотность заряда отрицательная, т.е. (-s), то линии напряжённости имеют противоположное направление.

Пример2.Определим поле между двумя плоскостями, равномерно с одинаковой плотностью заряженными разноимёнными зарядами (плоский конденсатор, рис.8). Считаем плоскости бесконечными.

Заряженная плоскость каждой пластины создаст по обе стороны от себя напря­женность поля, выражаемую формулой ±s/2e₀. Внутри металлических пластин и вне конденсатора эти поля направлены противоположно и поэтому в сумме дают нуль. Внутри конденсатора эти поля, напротив, направлены одинаково и, складываясь, дают у поверхности пластин напряженность Е = s/e₀. В данном частном случае электрическое поле од­нородно и поэтому его напряженность у поверхности пластин такая же, как и в других точках поля.