Напряжённость поля точечного заряда убывает обратно пропорционально квадрату расстояния от заряда.
Направление вектора `E определяется направлением силы `F, действующей на положительный заряд, помещённый в рассматриваемую точку поля, рис. 1.
q +1 `E


 -q `E +1
-q `E +1

Из сказанного следует, что если известна напряженность поля в какой-либо точке, то тем самым определена и сила, действующая на электрический заряд, помещённый в эту точку, а именно:
`F=q`E.
Если электрическое поле создается не одним, а несколькими точечными зарядами q1, q2, q3,…qn, то в этом случае результирующая напряженность суммарного силового поля равна
`E = `E1+`E2 +`E3 +…+`En = S`Ei.
т. е. вектор напряженности электрического поля системы зарядов равен геометрической сумме напряженностей полей, создаваемых в данной точке каждым из зарядов в отдельности( принцип суперпозицииэлектрических полей). Принцип суперпозиции выполняется лишь тогда, когда электрические поля не меняют свойств среды, т.е. пока внешние поля значительно меньше электрических полей, существующих внутри атомов и молекул.
Возможны случаи, когда электрическое поле создастся не точечным зарядом, а заряженным телом объема V. В этом случае необходимо знать распределение зарядов внутри тела.
Выделим внутри заряженного тела малый объём 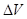 и обозначим через
и обозначим через 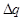 величину электрического заряда, находящегося в этом объёме.
величину электрического заряда, находящегося в этом объёме.
Предел отношения 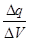 , когда величина объёма неограниченно уменьшается, называется объёмной плотностью электрических зарядовв данной точке. Обозначим её r.
, когда величина объёма неограниченно уменьшается, называется объёмной плотностью электрических зарядовв данной точке. Обозначим её r.
lim 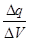 =r
=r
Т.о. объёмная плотность заряда измеряется зарядом единицы объёма тела. В общем случае неравномерно заряженного тела r различно в разных точках. Распределение заряда в объёме известно, если известно r как функция координат.
Очень часто заряды распределяются в телах только внутри тонкого поверхностного слоя. В этом случае удобно пользоваться поверхностной плотностью заряда s, которая определяется аналогично объёмной плотности зарядов
lim 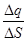 =s
=s
Величина заряда, находящегося на элементе поверхности dS, равна sdS. Для задания распределения зарядов на поверхности тела нужно знать s как функцию координат поверхности.
В случае линейного заряженного тела
lim 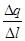 =l- линейная плотность заряда.
=l- линейная плотность заряда.
Во всех этих трёх случая, если известно распределение зарядов тела, то можно вычислить и электрическое поле, создаваемое этим телом. Для этого заряженное тело разбивают мысленно на бесконечно малые части и, рассматривая их как точечные заряды, вычисляют напряженность поля, создаваемую отдельными частями тела. Полное поле находят затем суммированием (интегрированием) полей, вызываемых отдельными частями тела, например:
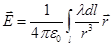
Дата добавления: 2015-10-19; просмотров: 1297;
