Пример 3. Равномерно заряженный шар.
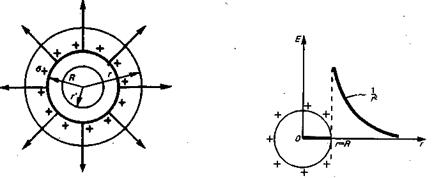
Рассмотрим электрическое поле между двумя шаровыми концентрическими электродами (рис.9) - шаровой конденсатор. Под действием взаимного притяжения (-) и (+ ) заряды расположатся только на поверхности внутреннего шара и на внутренней поверхности внешнего
|
Рис.9. Рис.10.
электрода. Из условий симметрии очевидно, что заряды на обоих шаровых электродах будут распределены равномерно, и что линии напряженности электрического поля могут быть только радиальными прямыми. Выберем в качестве замкнутой поверхности сферу с радиусом r, расположенную между электродами и имеющую общий центр с обоими электродами.
По теореме Остроградского-Гаусса
Ф = Е(r)4pr2 = q/e0,
откуда
Е(r)=q/4pe0r2. (*)
Эта формула показывает, что напряжённость поля между электродами зависит от расстояния r рассматриваемой точки поля от центра внутреннего шара, но не зависит вовсе от размеров внешнего электрода. Ту же напряженность поля получим, если радиус внешнего электрода будет как угодно велик. Роль внешнего электрода могут играть различные удалённые заземлённые предметы, например стены, пол и потолок комнаты. Поэтому часто говорят просто о поле заряженного шара(рис.10),не указывая, что именно является вторым электродом. Из формулы (*) следует, что электрическое поле шара, равномерно заряженного по поверхности, во внешнем пространстве совпадает с полем точечного заряда, равного полному заряду шара и помещённого в центре шара. Если бы мы рассмотрели шар, заряженный равномерно по объёму, то напряженность поля тоже выражалась бы формулой (*). Напряженность же поля внутри шара в обоих случаях различна. В случае шара, равномерно заряженного по поверхности Е = О в любой внутренней точке. Если же шар заряжен равномерно по объёму, то Е= 0 только в центре шара и с увеличением расстояния r от центра возрастает пропорционально r. В справедливости этого можно убедиться также при помощи теоремы Остроградского-Гаусса.
Пример: «клетка Фарадея».
металл
 ++++++++++++++++
++++++++++++++++
|
+ +
+ +
+ +
+ + + + + + + + + + + + + + +
Рис.11.
Дата добавления: 2015-10-19; просмотров: 2570;
