Затраты, выручка и прибыль

В общежитейском смысле оптимизация – нахождение наилучшего, оптимального. В частности, оптимизация прибыли – это нахождение таких способов функционирования фирмы, т.е. производства и реализации товаров или услуг, при которых разность между полными затратами и выручкой максимальна. В этом состоит основная цель деятельности фирмы. Затраты разнообразны и непостоянны, выручка также зависит от различных факторов, поэтому оптимизация прибыли – сложная, зачастую творческая, задача. Рассмотрим некоторые модели функционирования фирмы и способы нахождения оптимальной прибыли.

Основным объектом изучения экономических процессов является предприятие («фирма»), деятельность которого определяется объемом выпускаемой продукции R (штук, тысяч штук или комплектов изделий) и отпускной ценой Р. Взаимодействие между отдельными предприятиями, государством и рынком, а также многообразие выпускаемой продукции, опирается на модели деятельности отдельной фирмы, представляющие собой следующие «этажи» моделирования и анализа.

По параметрам Р и R (которые пока считаются независимыми) рассчитываются экономические показатели фирмы: выручка В, затраты Z, прибыль П, норма прибыли ρ и так далее.

При расчете экономических показателей необходимо иметь ввиду следующие обстоятельства.

Кроме цены производителя Р существуют цены потребителя:

Р₁=Р(1+q₁) (4.1)

Р₂=Р(1+q₁+α)=Р₁(1+α₁) (4.2),

где q₁ – доля налога на добавленную стоимость (фактически являющегося налогом с оборота), α– доля торговой наценки. Различие Р, Р₁ и Р₂ существенно потому, что в расчете прибыли фирмы торговая наценка не участвует, но спрос потребителя определяется ценой Р₁ или Р₂, которую ему приходится платить за товар.

Затраты Z на производство продукции являются монотонно возрастающей функцией объема производства:

Z = Z (R), Z′(R) > 0

т.е. большему значению объёма производства R соответствует большее значение затрат Z (рис. 4.9). Касательная к такой функции, имеет положительный угловой коэффициент (он равен тангенсу угла между этой касательной и осью объёма R). Угловой коэффициент равен производной, следовательно, производная тоже положительна. Таким образом, производная функции затрат в зависимости от объёма, положительна.

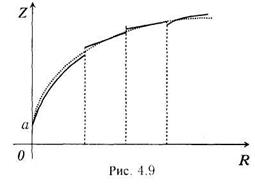
Но если ввести удельные затраты C(R) – затраты, отнесённые к объёму, – то они являются убывающей функцией объема R –иначе не было бы известного эффекта выгодности массового производства.

Если выделить постоянные слагаемые Z и C(R), то получим:

Z = a+Z₁(R),

Z₁(R) = RC(R) = R[a₀+C₁(R)] (4.3),

< 0.

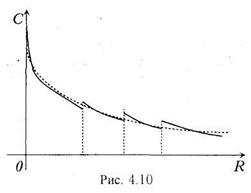
Функция удельных затрат убывает в зависимости от объёма, т.е. большему значению объёма соответствует меньшее значение затрат (рис. 4.10). Касательная к такой функции имеет отрицательный угловой коэффициент, следовательно, производная также отрицательна.

Вообще говоря, функция Z(R) не является непрерывной, т.к. при росте R возникает необходимость дополнительных единовременных затрат (строительство новых цехов и складов, покупка дополнительных станков и автоматических линий), могут иметься точки нарушения гладкости, «излома» (рис. 4.9) – например, если необходимо ввести дополнительного контролера.

Соответственно в этих точках разрыва непрерывности и излома имеет разрывы функция C₁(R) (рис. 4.10).

Поэтому строже было бы применять анализ в отдельности на каждом отрезке гладкости, но для упрощения расчетов целесообразно считать зависимости гладкими (т.е. их пунктирные кривые на тех же рисунках), а после получения рекомендаций по выбору оптимальных значений провести уточнённый поверочный расчет.

Имеется также и верхний предел объема R, превышение которого дает рост удельных затрат, но и это обстоятельство удобнее учитывать на втором этапе, при поверочных расчетах.

Выручка (доход) подсчитывается как произведение объема продаж S на цену проданной продукции, однако при этом необходимо учесть изымаемую государством сумму налога на добавленную стоимость и возвращаемую сумму налога на добавленную стоимость, выплаченную фирмой (как потребителем) при покупке комплектующих изделий С_n (на единицу или тысячу изделий), при этом не учитывается торговая наценка:

B = SP₁ – SPq₁+ SCn

( может быть отлично от q₁).

Величина затрат описана в формуле (4.3), где

а₀ = a₀₁+ C_n(1+ ),

поэтому выражение для прибыли (разности между доходоми затратами) имеет вид:

П = B – Z= S(P+C_n )–[a+R(a₀₁+C_n(1+ )+C₁(R))] (4.4)

S ≤ R.

Объем продаж определяется спросом D ипредложением R:

S = min(D, R),

(S равно меньшему из чисел D и R) поэтому рассмотрим два возникающих здесь случая: D ≥ R (дефицит) и D ≤ R (перепроизводство). В первом случае S = R и выражение для прибыли принимает вид:

П=RP–[a+R(a₀₁+C_n+C₁(R))] (4.5)

т.е. в расчете фактически не участвует НДС (ни q₁ ни ).

Во втором случае S = D ≤ R и возникают дополнительные затраты Z₂ на хранение непроданного товара R–D=и > 0. Затраты Z₂ зависят от разности между произведённым R и проданным D товаром и являются возрастающей функцией.

Z₂, Z'₂ > 0,

т.е.:

П = D(P+C_n )–[a+R(a₀₁+C_п(1+ )+C₁(R))+Z₂(R–D)] (4.6)

(q₁ не участвует в расчете, но учитывается, т.к. слагаемые DC_n , и –RC_n , не равны между собой и взаимно не уничтожаются).

Если формирование затрат связано с использованием банковского кредита (с учетной ставкой r для периода обращения капитала – от момента кредитования до момента продажи), то затраты Z (квадратная скобка в выражениях (4.4) и (4.6)) должны быть умножены на (1+r):

D ≥ R: П=RP–(1+r)[(a₀₁+C_n+C₁(R))R+a]–RC_n r

D ≤ R: П=D(P+С_n )–(1+r)[a+R(a₀₁+C_n(1+ )+C₁(R))+Z₂(R–D)] (4.7)

Норма прибыли (рентабельность) является отношением прибыли к затратам, т.е. 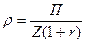и легко рассчитывается по приведенным формулам.

Целесообразно привести еще формулы для расчета чистой прибыли П₁ с учетом доли q₀ налога на прибыль и сбора W государства (включая в него суммы налога на прибыль, налога на добавленную стоимость и банковского сбора – считая банк государственным):

П₁=П(1–q₀) (4.8)

W=Пq₀+SPq₁–SС_n +Zr (4.9)

Впрочем, если учитывать, что «возвращаемая» фирме часть налога на добавленную стоимость все равно остается у государства, третье слагаемое может быть опущено.