Полезность и взаимозаменяемые товары

В экономических моделях понятия, отражающие субъективные черты покупателя, такие, как удовлетворение и благосостояние, описываются полезностью.

Пусть имеется множество товаров (i = 1, 2,…, п). Обозначим количество каждого товара x₁, ..., х_n. Пусть х₀ – количество денег у покупателя. Предположим, полезность каждого набора товаров можно оценить количественно. Такая оценка называется функцией полезности и. Это – функция, выражающая полезность в зависимости от товаров и их количества: и = и(х₀, х₁, ..., х_n).

Предельная полезность – это дополнительная полезность, полученная от дополнительной единицы товара. С помощью функции полезности она выражается так: предельная полезность i-го товара .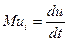

Рассмотрим пример. Пусть покупка одной плитки шоколада имеет для покупателя полезность 5 единиц (удовлетворения). Это – и общая и предельная полезность. Покупка второй плитки имеет меньшую полезность (т.к. уже имеется первая плитка), равную 4 единицы (это – предельная полезность второй плитки), тогда покупка двух плиток шоколада, первой и второй, имеет общую полезность 9 единиц и т.д. (см. табл. 3.1).

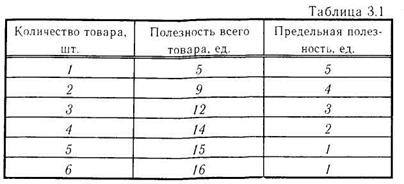
Полезность всего купленного шоколада равна сумме предельных полезностей каждой купленной плитки. Полезность всего товара возрастает, а предельная полезность убывает.

Предполагается, что покупатель стремится максимизировать полезность (удовлетворение), имея ограниченный доход, и что каждая последующая порция одного и того же товара имеет меньшую полезность, чем предыдущая.

Описанная модель удовлетворения покупателя основана на предположении, что полезность можно измерить количественно. Такая гипотеза называется кардинализмом. Предположение, что полезность различных товаров можно ранжировать только по порядку и разницу между ними нельзя выразить количественно, называется ординализмом.

Проанализируем выбор товаров покупателем. Покупателю необходимо выбрать некоторую комбинацию товаров. Пусть имеется всего два товара i = 1 и i = 2. Рассмотрим всевозможные наборы покупки этих товаров {x₁, x₂}, где x₁ – количество 1-го товара, x₂ – количество 2-го товара. Выберем из всех наборов имеющие равную суммарную полезность. Изобразим такие наборы графически. Пусть на оси x₁ отложено количество 1-го товара, а на оси x₂ – количество 2-гo. Точки, соответствующие равной суммарной полезности, составляют график, называемый кривой безразличия или изоквантой, т.к. покупателю безразлично, какой из наборов, лежащих на этой кривой, выбрать, они все имеют одинаковую полезность (рис. 3.4).

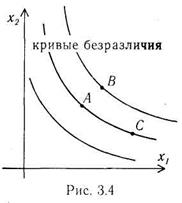
Рассмотрим наборы товаров, соответствующие точкам А, В и С на рис. 3.4. Наборы А и С имеют одинаковую полезность, т.к. лежат на изокванте. Набор В имеет большую полезность, чем набор А, т.к. в него входит больше товара x₁ и больше товара x₂. Поэтому набор В имеет большую полезность, чем набор С.

Через каждую точку плоскости x₁, x₂ проходит единственная изокванта. Т.е. для любой комбинации товаров найдутся другие комбинации, имеющие такую же суммарную полезность. Таким образом, имеется набор изоквант, соответствующих разным значениям суммарной полезности. Множество изоквант называется картой изоквант или картой безразличия покупателя.

Кривая безразличия всегда убывает, т.к. увеличение количества одного товара компенсируется уменьшением количества другого.

Предположим, товары x₁ и x₂ не являются независимыми. Например, чашки и блюдца или зажигалки и сигареты используются, как правило, совместно. Такие товары называются взаимодополнительными. Пусть товары x₁ и x₂ абсолютно взаимодополнительные, т.е. один товар не покупается без другого. Тогда изменение количества одного товара при сохранении неизменным количества другого не меняет полезности всего набора. Карта изоквант для этого случая изображена на рис. 3.5.

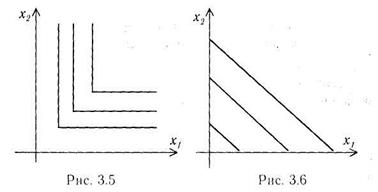
Другой случай зависимости товаров иллюстрируется, например, маслом и маргарином или кофе различных сортов. Один товар из такой пары может заменить другой, т.к. они предназначены для примерно одинаковых способов потребления. Такие товары называются взаимозаменяемыми. Пусть товары x₁ и x₂ абсолютно взаимозаменяемые, т.е. покупателю совершенно безразлично, какой товар приобрести. Тогда уменьшение количества одного товара соответствует такому же увеличению другого товара и наоборот, а изокванты – прямые линии. Карта изоквант в этом случае изображена на рис. 3.6. Случаи абсолютной взаимозаменяемости и взаимодополнительности не являются типичными для практики. Чаще имеется некоторая зависимость товаров и ей соответствует изокванта, качественно представленная на рис. 3.4.

Выбор товаров покупателем зависит также и от имеющихся у него средств – К. Возникает бюджетное ограничение:если цена товара х_i равна Р_i то количество купленного товара должно удовлетворять неравенству

Р₁х₁ + Р₂х₂ + ... + Р_nх_n ≤ К.