Задача 4. Кинематический анализ структурной группы

II класса 4 вида

Исходные данные для расчета: υ_D3 (м/с), υ_D6 = 0; а_D3 (м/с²), а_D6 = 0; ω₃, ξ₃.

Определить: υ_D5 (м/с), а_D5 (м/с²).

Решение. Построение плана скоростей. В точке D соединяются четыре звена (3 - кулиса, 4 - кулисный камень, 5 - ползун, 6 - опора). Поэтому будет четыре точки: D₃, D₄, D₅, D₆. При этом υ_D3 ¹ υ_D4 ,υ_D5 ¹ υ_D6 - т.к. поступательные кинематические пары; υ_D4 = υ_D5 - т.к. вращательная кинематическая пара; ω₅ = ω₆ = 0, ξ₅ = ξ₆ =0 - т.к. 5-ое звено движется поступательно, а 6-ое звено неподвижно (опора).

а) б) в)

у d_4,5 υ_D5 P_υ d_4,5 а_D5 P_а

D (D₃, D₄, D₅, D₆) а_D4D3

3 5 6 а^r_D4D3 а_D3

х 4 х υ_D3D4 υ_D3 d₃

d₃ k а^к_D4D3

υ_D3 а_D3 у

ω₃, ξ₃

а – структурная группа; б - план скоростей; в - план ускорений

Рисунок 2.10 - К кинематическому расчету структурной группы II класса 4 вида

После расчета масштабного коэффициента скорости по формуле

μ_υ = υ_D3 / [P_υd₃] (2.53)

записываются векторные уравнения скоростей:

υ_D4 = υ_D3 + υ_D4D3 êêу-у

υ_D5 = υ_D6 + υ_D5D6 êêх-х. (2.54)

Из полюса P_υ откладывается заданное направление вектора скорости точки D₃. Затем из точки d₃ проводится линия, параллельная у-у, а из полюса – линия, параллельная х-х (рисунок 2.10). На пересечении получается точка d₄ = d₅. После построения высчитываются действительные значения скоростей:

υ_D3D4 = [d₃d₄] μ_υ; υ_D5 = [P_υd₅] μ_υ= (м/с). (2.55)

Построение плана ускорений начинается с расчета масштабного коэффициента

μ_а = а_D3 / [Р_аd₃] = ( 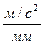). (2.56)

Векторные уравнения имеют вид:

а_D4 =а_D3 + а^к_D4D3 + а^r_D4D3 || у-у

а_D5 = а_D6 + а^к_D5D6 + а^r_D5D6 || х-х. (2.57)

Кориолисово ускорение высчитывается по формуле:

а^к_D3D4 = 2 ω₄ υ_D3D4; а^к_D5D6 =0. (2.58)

Вектор а^к_D3D4 направлен перпендикулярно 3-му звену в сторону угловой скорости ω₃; релятивные ускорения направлены параллельно осям у-у и х-х. После построения высчитываются действительное значение ускорения

а_D4,5 = [P_аd₅]µ_а = (м/с²). (2.59)

Задача 5. Кинематический анализ структурной группы

II класса 5 вида

Исходные данные: υ_D3, υ_D6 = 0; ω₃ = ω₆ = 0; а_D3 = а_D6 = 0.

Определить: υ_D5, а_D5.

Решение. Построение плана скоростей. Также как и в Задаче 4, в точке D соединяются четыре звена. Поэтому будут четыре точки: D₃, D₄, D₅, D₆ (рисунок 2.11). После расчета масштабного коэффициента скорости по формуле (2.30) записываются векторные уравнения-формулы (2.54). Построение плана скоростей ведется аналогично Задаче 4. Угловые скорости звеньев 4 и 5 равны нулю, т.к. они движутся поступательно (ω₄ = ω₅ = 0). Рассчитывается скорость точки D₅ по формуле (2.54). Строится план ускорений. Высчитывается масштабный коэффициент плана ускорений по формуле (2.56). Затем записываются векторные уравнения – формулы (2.57). В данном случае кориолисово ускорение а^к_D3D4 = 0, т.к. ω₄ = 0.

Построение плана ускорений ведется аналогично Задаче 4. В конце рассчитывается ускорение точки D₅ по формуле (2.59).

а) б) в)

х

у 6 5 у υ_D5 а_D5

P_υ d₅ d₅ P_a

D(D₃,D₄,D₅,D₆) 4 υ_D3 υ_D5D3 а_D5D3 а_D3

3 υ_D3 d₃ d₃

a_D3

х

а – структурная группа; б - план скоростей; в - план ускорений

Рисунок 2.11 - К кинематическому расчету структурной группы II класса 5 вида

Итак, мы рассмотрели определение скоростей и ускорений методом планов для всех видов структурных групп. Пример кинематического расчета шестизвенного механизма будет приведен в главе 3, п. 3.1.8. А теперь подведем некоторые итоги по правилам построения планов.

Свойства планов скоростей, ускорений

1. Векторы всех полных (абсолютных) скоростей (ускорений) имеют своим началом точку полюса, а векторы относительных скоростей (ускорений) соединяют собой концы векторов полных скоростей (ускорений).

2. Векторы полных скоростей (ускорений) всегда направлены от полюса. Векторы относительных скоростей (ускорений) направлены так, чтобы удовлетворялись векторным уравнениям (т.е. к той точке, которую строим).

3. Скорости (ускорения) точек подобных фигур (жестких треугольников или отрезков) находятся по правилу подобия (см. Задачи 1 и 2).

4. Точки, скорости и ускорения которых равны нулю, находятся в полюсе.

5. При плоскопараллельном движении векторы относительных ускорений образуют со звеном угол μ, тангенс которого равен tg μ = ξ / ω².