Методом построения кинематических диаграмм

При кинематическом исследовании механизма необходимо определять скорости и ускорения за полный цикл движения механизма. Для этого исследование проводится для ряда положений механизма, достаточно близко отстоящих друг от друга. По полученным значениям строятся графики, носящие названия кинематических диаграмм.

Кинематические диаграммы - графики зависимости перемещения S, скорости V и ускорения a от времени t или от угла поворота φ, а именно

S = f(t); υ =f(t); a= f(t).

В зависимости от характера движения исследуемых звеньев или отдельных точек механизма могут быть построены и различные кинематические диаграммы. Например, если известен ход поршня (ползуна), то можно построить диаграмму перемещения, а по ней методом графического дифференцирования строятся графики скорости и ускорения. Если же задается диаграмма ускорения ведомого звена, то методом графического интегрирования строятся графики скорости и перемещения.

Задача 1. Метод графического дифференцирования

Графическое дифференцирование можно проводить методом касательных или методом хорд. Метод касательных имеет более низкую точность по сравнению с методом хорд.

Метод хорд предполагает замену заданной кривой ломаной линией, т.е. полученные точки соединяют хордами. При этом принимают следующее допущение: угол наклона касательных в точках, расположенных посередине каждого участка кривой, равен углу наклона соответствующей хорды. Это допущение вносит некоторую погрешность, но она относится только к данной точке. Эти погрешности не суммируются, что обеспечивает большую точность метода по сравнении с методом касательных.

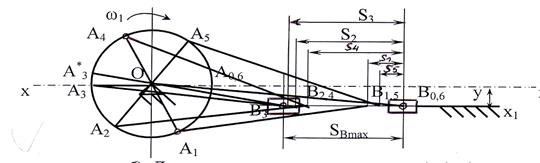
Рассмотрим на примере кривошипно-ползунного механизма (рисунок 2.1). Изобразим кривошипно-ползунный механизм в 6-и положениях, начиная с крайних (см. гл. 2. §2.2). Затем делим траекторию движения точки А (окружность радиусом ОА) от точки А₀ на 6 частей в сторону вращения (рисунок 2.12). Получаем точки А₁, А₂, А₃ и т.д. Из полученных точек радиусом АВ делаем засечки на траектории движения точки В. Получаем точки В₁, В₂, В₃ и т.д. Второе крайнее положение не совпало с разбивкой, поэтому его нужно достроить. Переходим к построению диаграммы перемещения.

Построение диаграммы перемещения. Строим оси координат S-t. Ось абсцисс (времени t) делим на 6 равных частей. Диаграмму перемещения можно строить в масштабе μ_S = μ_ℓ. Для этого замеряем расстояния от точки В₀ до точек В₁, В₂ и т.д. Получаем расстояния S₁ = h₁, S₂ = h₂ и т.д., которые откладываем по вертикали.

Расстояние S_max должно равняться h_max. Если же получается слишком низкий или очень высокий график, то масштабный коэффициент считают заново:

μ_S = S_max μ_ℓ / h_max, (2.60)

где h_max выбирают нужной величины. Затем считают высоты h₁ = S₁ μ_ℓ /μ_S = (мм), h₂ и т.д.

Mаксимум на графике перемещения должен соответствовать второму крайнему положению. Поэтому, находим на оси t точку 3*. Для этого определим отрезок [3-3*] из пропорции:

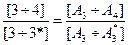
и от полученной точки (3*) откладываем вверх высоту h_max.

Приступаем к построению диаграмм скоростей и ускорений методом графического дифференцирования.

Для построения диаграммы скорости продолжаем ось ОS вниз. Горизонтально проводим ось t и делим ее на те же равные 6 частей. Влево от точки О произвольно откладываем полюсное расстояние Н₁=[ОР₁] (чем больше полюс, тем выше будет диаграмма скоростей). Параллельно хордам 0-1, 1-2, 2-3 и т.д. из полюса Р₁ проводим лучи и на серединах каждого участка отмечаем точки 1¢, 2¢, 3¢ и т.д. Соединяем все точки плавной линией. Заметим: максимальному значению ординаты диаграммы перемещения соответствует нулевое значение ординаты диаграммы скорости.

Имея диаграмму скоростей аналогично можно построить диаграмму ускорений, дифференцируя первую. Нужно отметить, что первая и последняя точки получатся на ¼ первого и последнего участков, остальные же точки должны получится на делительных отрезках.

Схема механизма μ_ℓ = ℓ_ОА/ОА = (м/мм)

S Диаграмма перемещения μ_S =…= (м/мм)

3 max

2 h₃ 4

h_max

h₂

1 h₄ 5

h₁ h₅

0 1 2 3 3* 4 5 6 t

Диаграмма скорости μ_V=…= (^м/с/_мм)

V

2^΄

3^΄

1^΄ h'₁ h'₂

Р₁

0 1 2 3 * 4 h'₄ h'₅ 5 6 t

4^΄ 6^΄

Н₁ 5^΄

Диаграмма ускорения μ_а=…= (^м/с2/_мм)

а

h''₀ h''₁ h''₅ h''₆

Р₂ 0 1/4 1 2 3 4 5 1/4 6 t

h''₂ μ_t=…= (^с/_мм)

h''₃

Н₂

Рисунок 2.12 - Построение диаграмм методом графического

дифференцирования с помощью хорд

Также нужно учесть, что возрастающим координатам диаграммы скорости соответствуют положительные значения ординат диаграммы ускорения, а убывающим ординатам – отрицательные. Хорды ускорений вписываются по средним значениям скоростей.

После построения диаграмм высчитываются масштабные коэффициенты:

t_дейст = 2π/ω₁ = (с);

μ_t = t_дейст /[0-6] = (с/мм);

μ_υ = μ_S/H₁μ_t = (^м/с/_мм); (2.61)

μ_а = μ_υ/H₂μ_t =(^м/с2/_мм),

где: Н₁, Н₂ – полюсные отрезки, взятые с чертежа в мм.

Для того чтобы посчитать действительные значения перемещений, скоростей и ускорений, необходимо замерить ординаты в мм на делительных отрезках и умножить на соответствующий масштабный коэффициент.

Задача 2. Метод графического интегрирования

Метод графического интегрирования - метод, обратный графическому дифференцированию. По заданной диаграмме ускорения строятся диаграммы скорости и перемещения. Если смотреть на графики снизу вверх (см. рисунок 2.12), то получатся нужные нам диаграммы. Рассмотрим на примере.

Пример. По заданной диаграмме ускорения определить максимальную скорость и максимальное перемещение методом графического интегрирования.

Задано: диаграмма ускорения 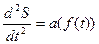, максимальное ускорение а_max (м/с²), время t (c).

Определить: максимальную скорость υ_max (м/с), максимальное перемещение S_max (м).

Решение. Перечерчиваем заданную диаграмму ускорения в произвольном масштабе (рисунок 2.13), при этом высоту h¢¢ выбираем произвольно. Высчитываем масштабные коэффициенты ускорения и времени

μ_а = а_max/ h¢¢ = ( );.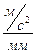

μ_t = t/ [0÷6] = ( ),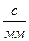

где [0÷6] – отрезок оси времени в мм.

Строим диаграмму скорости методом графического интегрирования. Для этого слева от оси ординат выбираем произвольнополюсное расстояние Н₁ (чем больше Н₁ тем положе и ниже будет график скорости).

Делим участки [0÷1], [1÷2] [2÷3] и т.д. пополам, проводим вверх до пересечения с графиком и соединяем с полюсом Р₁. Полученные линии параллельно переносим на соответствующие участки диаграммы скорости. Аналогично строим диаграмму перемещения.

Масштабные коэффициенты диаграмм будут рассчитываться по следующим формулам:

μ_V = μ_aμ_tH₁ = (^м/с/_мм); (2.62)

μ_S= μ_Vμ_tH₂ = (м/мм),

где H₁, H₂ – полюсные расстояния, замеренные с диаграмм в мм.

Определяем максимальные действительные значения скорости и перемещения

υ_max = h¢·μ_V =(м/с); S_max = h·μ_S =(м).

Более подробно построение диаграмм этим методом будет рассказано в главе 4, §1, п. 1.4.

Итак, мы рассмотрели кинематическое исследование плоских рычажных механизмов графоаналитическими методами. Это позволяет представить движение отдельных точек звеньев механизма более наглядно. Теперь приступим к изучению работы механизма под действием заданных сил.

Вопросы для самопроверки

1. Постройте в крайних положениях выходного звена кривошипно-ползунный механизм, шарнирный четырехзвенный и кулисный механизмы.

2. Расскажите о преимуществах и недостатках определения скоростей и ускорений методом планов.

3. Укажите порядок построения планов скоростей и ускорений в многозвенном механизме.

4. Расскажите, как, пользуясь планом скоростей, определить величину и направление угловой скорости звена?

5. Как, пользуясь планом ускорений, определить величину и направление углового ускорения?

6. Объясните правило подобия для определения скорости (ускорения) какой-либо точки звена.

7. При каких движениях звена возникает кориолисово ускорение? Как определить его величину и направление?

8. Расскажите о преимуществах и недостатках определения скоростей и ускорений методом построения кинематических диаграмм.

9. Какие характерные точки позволяют проверить правильность построения диаграмм?