Точек звеньев механизма
Рассмотрим определение скоростей и их направлений для разного вида движений.
а). Звено движется поступательно.
В этом случае скорость и ускорение направлены по траектории движения ползуна. Если ускорение направлено по движению скорости, то движение называется ускоренным; если направления их не совпадают, то движение является замедленным.
|
 | |||
 |
б). Звено движется вращательно с постоянной угловой скоростью.
Здесь вектор скорости точки А направлен перпендикулярно звену ОА в сторону ω1. Скорость точки А вычисляется по формуле
υА = ω1ℓОА = (м/с). (2.26)
Т.к. угловая скорость звена постоянная величина, то угловое ускорение равно нулю ξ1 = 0, а, следовательно, и тангенциальное ускорение также равно нулю: аτОА= ξ1ℓОА= 0.
|

 А
А
 аА υА
аА υА
 |

 О ω1
О ω1
 |
в). Звено совершает неполное вращательное (качательное) движение. При этом движении скорость точки В вычисляется по формуле υВ = ω3ℓВС, а ее вектор направлен перпендикулярно звену ВС в сторону угловой скорости.
|

 аτВС В
аτВС В

 аВ υB
аВ υB
 аnВС
аnВС

 С ξ3
С ξ3





 ω3
ω3
Тангенциальное ускорение определяется из формулы:
аτВС = ξ3ℓВС = (м/с2) (2.29)
и направлено перпендикулярно звену ВС в сторону углового ускорения ξ3.
Определение скоростей и ускорений структурных групп осуществляется графоаналитическим способом, т.е. построением планов скоростей и планов ускорений.
Определение скоростей и ускорений методом планов
План скоростей (ускорений) – чертеж, на котором изображены в виде отрезков векторы, равные по модулю и по направлениям скоростям (ускорениям) различных точек звеньев механизма.
План скоростей (ускорений) для механизма является совокупностью нескольких планов скоростей (ускорений) для отдельных групп Ассура, а значит, и отдельных звеньев. При построении планов скоростей (ускорений) используются известные из теоретической механики теоремы о сложении скоростей и ускорений.
Правила построение планов
1. Построение планов ведется по векторным уравнениям в порядке присоединения групп Ассура к ведущему звену.
2. Планы скоростей (ускорений) строятся из одного полюса. Рυ - полюс плана скоростей; Ра - полюс плана ускорений (см. п. 2.1.).
3. Скорости и ускорения внешних шарниров должны быть известны и ранее определены. Необходимо определить скорости внутренних шарниров.
3. Концы векторов скоростей (ускорений), т.е. концы стрелок, обозначаются теми же буквами (только малыми), что и кинематические пары (точки) на механизме.
4. Концы нормальных ускорений имеют индекс n, кориолисовых k, тангенциальных (касательных) τ, релятивных (относительных) r.
Рассмотрим построение планов скоростей и ускорений для каждой структурной группы.
Задача 1. Кинематический анализ структурной группы
II класса 1 вида
Исходные данные для расчета:
ℓАВ, ℓВС, ℓВЕ = ℓСЕ - длины звеньев в м; υА, υС - скорости внешних шарниров (направление и величина) в м/с; аА, аС - ускорения внешних шарниров (направление и величина) в м/с2.
Определить: υВ, аВ - направление и величина скорости и ускорения внутреннего шарнира; ω2, ω3 - угловые скорости звеньев; ξ2, ξ3 - угловые ускорения звеньев; υЕ, аЕ - скорость и ускорение точки Е.
Общие сведения. В точке В соединены 2 звена. Поэтому будут две точки В: В2, принадлежащая второму звену, и В3, принадлежащая третьему. Если звенья соединены во вращательную кинематическую пару, то линейные скорости и ускорения будут равны, а угловые нет, т.е.
υВ2 = υВ3, а В2 = а В3, ω2 ¹ ω3, ξ2 ¹ ξ3.
Решение. Рассчитывается масштабный коэффициент плана скоростей
μυ = υА/[Рυа] = (м/с), (2.30)
причем отрезок [Рυа] выбирается произвольно.
Затем считается чертежная величина вектора скорости точки С
[Рυс] = υС /μυ = (мм). (2.31)
Построение плана скоростей. На свободном поле чертежа выбирается точка полюса Рυ. Из нее строятся заданные или заранее определенные отрезки скоростей [Рυа] и [Рυс] (рисунок 2.6). Для определения скорости точки В движение этой точки раскладывается на переносное поступательное со скоростями точек А и С и относительное вращательное вокруг этих же точек. Тогда, воспользовавшись сложением скоростей, векторные уравнения будут иметь вид:
 υВ = υА+ υВА ^ АВ;
υВ = υА+ υВА ^ АВ;
υВ = υС + υВС ^ ВС. (2.32)



 В(В2,В3) а υА Рυ
В(В2,В3) а υА Рυ




 υВ υС
υВ υС

 2 3 ω3 с
2 3 ω3 с



 υВА υЕ
υВА υЕ


 А Е С е
А Е С е



 1 ω2 4 в υВС
1 ω2 4 в υВС
υА υС
Рисунок 2.6 - Схема структурной группы II класса 1 вида
и ее план скоростей
Направления относительных скоростей известны по направлению: υВА ^ АВ, υВС ^ ВС. Величины этих скоростей будут находиться из построения плана скоростей. Для этого из точки а на плане скоростей проводится линия действия скорости υВА, перпендикулярная звену АВ, а из точки в проводится линия действия вектора скорости υВС, перпендикулярная звену ВС. На пересечении получается искомая точка в.
Точка е на плане скоростей определяется по правилу подобия:
1. если на схеме механизма имеется жесткий треугольник (ΔВСЕ), то на плане скоростей (ускорений) будет подобный треугольник (Δвсе), причем порядок букв на схеме механизма будет совпадать с порядком букв на плане скоростей или ускорений (обход контура);
2. если точка находится на звене и делит его на пропорциональные отрезки, то данная точка на плане скоростей(ускорений) будет находиться на соответствующем векторе и делить его на равнозначные пропорциональные отрезки;
3. если точка находится на продолжении звена, то на плане скоростей (ускорений) она будет находиться на продолжении соответствующего вектора, причем порядок букв на схеме механизма будет совпадать с порядком букв на плане скоростей или ускорений.
Воспользуемся п.1 из правила подобия. Так как по заданию ℓВЕ = ℓСЕ, то и отрезки ве = се. Длина этих отрезков определится из пропорции
ℓВЕ/ℓВС=ве/вс. (2.33)
Теперь из точек в и с проводятся дуги до их пересечения, равные этим отрезкам. Получается искомая точка в.
 Определяются действительные значения всех найденных векторов скоростей:
Определяются действительные значения всех найденных векторов скоростей:
υВ = [Рυв]μυ =
υЕ = [Рυе]μυ = (м/с).
υВА = [ав]μ υ=
υВС = [вс]μυ =
Отрезки замеряются на плане скоростей в мм и умножаются на масштабный коэффициент плана скоростей.
После определения линейных скоростей определяются угловые скорости:
 ω2 = υ2ВА/ℓАВ = (с-1),
ω2 = υ2ВА/ℓАВ = (с-1),
ω3 = υ2ВС/ℓВС = (2.34)
а затем и их направления.
Определим направление угловой скорости ω2. Для этого вектор линейной скорости υВА мысленно переносим во внутренний шарнир на схеме механизма, т.е. в точку В, и вращаем точку В относительно точки А (точку А считаем неподвижной). Аналогично определяем направление ω3.
Построение плана ускорений. Рассчитываем масштабный коэффициент плана ускорений:
μа = аА/[Раа] = (м/с2/мм). (2.35)
Затем высчитываем чертежную величину вектора ускорения точки С:
[Рас] = аС/µа = (мм). (2.36)
На свободном поле чертежа произвольно выбирается точка полюса Ра. Из нее проводятся ранее определенные отрезки [Раа] и [Рас] (рисунок 2.7).
Для определения ускорения внутреннего шарнира (точки В) рассматриваем ее сложное движение. Сложное движение состоит из переносного поступательного с ускорениями аА и аС, и относительного вращательного вокруг точек А и С. Тогда векторные уравнения для определения ускорения точки В будут следующие:
 аВ = аА + аnВАêêАВ + аτВА^АВ
аВ = аА + аnВАêêАВ + аτВА^АВ
аВ = аС + аnВСêêВС + аτВС^ВС (2.37)
 В а аА Ра
В а аА Ра






 аnВА
аnВА


 2 3 nВА аС
2 3 nВА аС
ξ 2 ξ 3 аВА аВ с



 А Е аnВС
А Е аnВС


 аА С аτВА e nВС
аА С аτВА e nВС
1 
 аС 4 аτВС
аС 4 аτВС
в
Рисунок 2.7 - Схема структурной группы II класса 1 вида
и ее план ускорений
В уравнении (2.37) известны направления всех векторов: нормальные ускорения направляются параллельно звеньям к центру вращения, а тангенциальные - перпендикулярно этим же звеньям. Величины нормальных ускорений находятся по формулам в (м/с2):
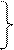 аnВА= υ2ВА/ℓАВ =
аnВА= υ2ВА/ℓАВ =
аnВС = υ2ВС/ℓВС = (2.38)
Вычисляем чертежные значения нормальных ускорений в мм:
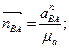
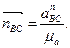 (2.39)
(2.39)
Тангенциальные ускорения определяются построением плана ускорений.
Из точки а на плане ускорений откладываем вектор 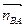 êêАВ и направляем его к точке А. Затем из точки nВА проводим линию действия тангенциального ускорения аτВА^АВ. Через точку с проводим вектор
êêАВ и направляем его к точке А. Затем из точки nВА проводим линию действия тангенциального ускорения аτВА^АВ. Через точку с проводим вектор 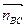 êêВС и направляем его к точке С, а из точки nВС проводим линию действия тангенциального ускорения аτВС ^ ВС. Пересечение этих линий даст искомую точку в иопределит длины векторов тангенциальных ускорений. Точку е найдем по п.1 правила подобия. Для этого составим пропорцию: ℓВС/ℓВЕ = вс/ве и строим аналогично скорости. Действительные значения ускорений определяются по формулам:
êêВС и направляем его к точке С, а из точки nВС проводим линию действия тангенциального ускорения аτВС ^ ВС. Пересечение этих линий даст искомую точку в иопределит длины векторов тангенциальных ускорений. Точку е найдем по п.1 правила подобия. Для этого составим пропорцию: ℓВС/ℓВЕ = вс/ве и строим аналогично скорости. Действительные значения ускорений определяются по формулам:
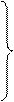 аВ= [Рав] μа = (м/с2);
аВ= [Рав] μа = (м/с2);
аЕ = [Рае] μа = (м/с2);
аτВА = [nВАв] μа = (м/с2); (2.40)
аτВС = [nВСв] μа = (м/с2).
Величина угловых ускорений определяется по формулам:
 ξ2 = аτ ВА/ℓАВ = (с-2);
ξ2 = аτ ВА/ℓАВ = (с-2);
ξ3 = аτ ВС/ℓВС = (с-2). (2.41)
Для определения направления угловых ускорений необходимо векторы этих ускорений мысленно приложить во внутренний шарнир и поворачивать звенья относительно точек А и С (рисунок 2.7).
Задача 2. Кинематический анализ структурной группы
II класса 3 вида
Исходные данные для расчета:
ℓОВ - межосевое расстояние (м),
ℓВD - длина кулисы (м);
υА1, υВ = 0 – величина и направления скоростей внешних шарниров (м/с);
величина и направления ускорений внешних шарниров аА1, аВ = 0 (м/с2).
Определить:
υА3, аА3 - направление и величину скорости и ускорения внутреннего шарнира;
ω 3, ξ 3- величину и направление угловых скорости и ускорения кулисы;
υD, аD - скорость и ускорение точки D.
Общие сведения. В точке А соединяются три звена, поэтому будет три точки: точка А1, принадлежащая первому звену; точка А2, принадлежащая второму звену и точка А3, принадлежащая третьему звену (рисунок 2.8). Как было указано в Задаче 1, если звенья соединены во вращательную кинематическую пару, то линейные скорости и ускорения этих звеньев равны, а угловые нет, т.е.
υА1 = υА2, аА1 = а А2; ω1 ¹ ω2;ξ1 ¹ ξ2.
Если звенья соединены в поступательную кинематическую пару, то линейные скорости и ускорения не равны между собой, а угловые равны, т.е.
υА2 ¹ υА3, а А2 ¹ а А3; ω2 = ω3; ξ2 = ξ3.
а) D б) в)

 3
3

 d а3 d а3 аА3
d а3 d а3 аА3




 υА1 υА3А2 υА3 аrА3А2 Ра
υА1 υА3А2 υА3 аrА3А2 Ра 











 аА1 А(А1,А2,А3) Рυ nА3В аnА3В
аА1 А(А1,А2,А3) Рυ nА3В аnА3В


 2 а1,2 υА1 kА3А2 аА1 а tА3В
2 а1,2 υА1 kА3А2 аА1 а tА3В
 а кА3А2 а1,2
а кА3А2 а1,2
 В ω3
В ω3
 4 ξ3
4 ξ3
а - схема структурной группы; б - план скоростей; в - план ускорений
Рисунок 2.8 - К кинематическому анализу структурной группы II класса 3 вида
Решение. Рассчитывается масштабный коэффициент плана скоростей:
μυ= υА1 / [Pυа1].
Построение плана скоростей. На свободном поле чертежа из полюса строим вектор скорости точки А1 (рисунок 2.8, б).
 Определим скорость точки А3. Особенность группы Ассура 3-го вида заключается в том, что переносным движением является вращательное движение кулисы 3 вокруг точки В, а поступательным является движение кулисного камня 2 по кулисе 3. Из этого следует, что абсолютная скорость точки А3 равна сумме двух скоростей: поступательной и вращательной. Поэтому уравнения примут вид:
Определим скорость точки А3. Особенность группы Ассура 3-го вида заключается в том, что переносным движением является вращательное движение кулисы 3 вокруг точки В, а поступательным является движение кулисного камня 2 по кулисе 3. Из этого следует, что абсолютная скорость точки А3 равна сумме двух скоростей: поступательной и вращательной. Поэтому уравнения примут вид:
υА3 = υА2 + υА3А2 êêАВ;
υА3 = υВ + υА3В ^ АВ. (2.42)
В этой системе известны все направления векторов скоростей. Из точки а1 на плане скоростей проводим линию действия υА3А2 êêАВ, а из полюса Рυ (т.к. υВ=0) – линию действия скорости υА3В ^ АВ. Запомните! Если скорость и ускорение точки равна нулю, то данная точка на плане скоростей или ускорений находится в полюсе! На пересечении двух линий действия получается точка а3.
Точка D на схеме структурной группы находится на продолжении звена АВ. Поэтому ее скорость будем определять по п.3. правилаподобия (Задача 1).Следовательно, будет иметь место следующая пропорция:
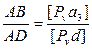 . (2.43)
. (2.43)
Определяя отрезок [Рυd] в мм, откладываем его на продолжении вектора [Рυа3]. На конце этого вектора отмечаем точку d.
 Вычисляем действительные значения найденных скоростей:
Вычисляем действительные значения найденных скоростей:
υА3 = [Pυа3]μυ = (м/с);
υА3А2 = [аА3аА2]μυ = (м/с); (2.44)
υD = [Pυd]μυ = (м/с).
Определяем величину и направление угловой скорости
ω3 = υ2А3В/ℓАВ, (2.45)
где ℓАВ = АВ·μℓ = (м) – действительная длина звена АВ. Направление угловой скорости ω3 определяется аналогично Задаче 1.
Построение плана ускорений. Величина и направление ускорений внешних шарниров известны (аА1, аВ = 0 в м/с2). Поэтому определяем масштабный коэффициент плана ускорений:
μа = аА1 / [Раа1] = (м/с2/мм). (2.46)
Абсолютное ускорение точки а3 равно сумме трех ускорений: переносного, относительного (релятивного) и кориолисова. Поэтому уравнение будет иметь вид:
 аА3 = аА2 + акА3А2 + аrА3А2;
аА3 = аА2 + акА3А2 + аrА3А2;
аА3 = аВ + аnА3В + аtА3В. (2.47)
В этой системе направления всех векторов известны, а именно: аnА3В || АВ и направлено к центру вращения (к точке В), аtА3В ^ АВ, аrА3А2 || АВ. Для определения направления кориолисова ускорения необходимо вектор относительной скорости υА3А2 повернуть вокруг его начала на 90о в сторону угловой скорости ω3. Величины кориолисова и нормального ускорений определяются по формулам:
акА3А2 = 2 ω3 υА3А2 = (м/с2); аnА3В = υ2А3В /ℓАВ = (м/с2). (2.48)
Определим вектора этих ускорений в мм:
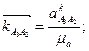
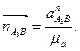 (2.49)
(2.49)
Из полюса Ра проводим вектор ускорения точки А1=А2 - отрезок [Раа1]. Из точки а1 проводим вектор кориолисова ускорения 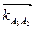 ^ АВ влево. Через точку kА3А2 проводим линию действия относительного (релятивного) ускорения аrА3А2 параллельно звену АВ. Затем из полюса Ра (т.к. аВ = 0) откладываем вектор нормального ускорения
^ АВ влево. Через точку kА3А2 проводим линию действия относительного (релятивного) ускорения аrА3А2 параллельно звену АВ. Затем из полюса Ра (т.к. аВ = 0) откладываем вектор нормального ускорения 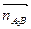 параллельно звену АВ вниз и, далее проводим линию действия тангенциального ускорения аtА3В перпендикулярно звену АВ. На пересечении линий действия релятивного и тангенциального ускорений получается точка а3. Точку d находим аналогично плану скоростей по правилу подобия. Из пропорции (2.43) определяем отрезок [Раd] и откладываем его на продолжении вектора [Раа3]. Находим действительные значения всех линейных ускорений:
параллельно звену АВ вниз и, далее проводим линию действия тангенциального ускорения аtА3В перпендикулярно звену АВ. На пересечении линий действия релятивного и тангенциального ускорений получается точка а3. Точку d находим аналогично плану скоростей по правилу подобия. Из пропорции (2.43) определяем отрезок [Раd] и откладываем его на продолжении вектора [Раа3]. Находим действительные значения всех линейных ускорений:
 аА3 = [Раа3] μа = (м/с2);
аА3 = [Раа3] μа = (м/с2);
аD = [Pаd] μа = (м/с2); (2.50)
аtА3В = [n1а3] μа =(м/с2).
Определяем величину углового ускорения кулисы 3:
ξ3 = аtА3В /ℓАВ = (с-2). (2.51)
Для определения направления ξ3 нужно вектор тангенциального ускорения аtА3В приложить в точку А на механизме и посмотреть, в какую сторону точка А вращается относительно точки В. Видно, что направление ξ3 получилось против часовой стрелки (рисунок 2.8).
Построение планов скоростей и ускорений 2, 4 и 5-го видов рассмотрим более кратко.
Дата добавления: 2015-10-19; просмотров: 861;
