Нескольких переменных

Вспомним теорему Вейерштрасса о том, что всякая непрерывная на ограниченном замкнутом множестве функция принимает на этом множестве наибольшее и наименьшее значения:

.

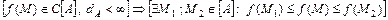Говорят, что в точках M₁, М₂ функция имеет глобальные экстремумы (в точке M₁ – глобальный минимум, в точке М₂ – глобальный максимум).

В R в качестве замкнутого множества обычно рассматривается отрезок [a, b], в R² – замкнутая связная (т.е. состо­ящая из одного «куска») область на плоскости, в R³ – замкнутое тело.

Точки глобальных экстремумов могут располагаться:

1) внутри [А] (тогда они совпадают с точками локальных экстремумов);

2) на границе [А] (совпадают с точками условных экстремумов).

Рассмотрим, например, схему поиска глобальных экстремумов для функции двух переменный в криволинейном треугольнике ( см. рисунок):

1) найти точки локальных экстремумов P_i внутри [А];

2) найти точки условных экстремумов Q_i на граничных кривых j_k(x, y)=0;

3) вычислить и сравнить значения целевой функции в точках P_i , Q_i и R_i .

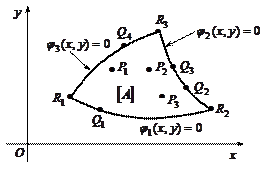С увеличением количе­ства переменных и усложне­нием формы множества [А] поиск глобальных экстремумов сопровождается возрастанием количества вычислений. В связи с этим для решения подобных экстремаль- ных задач частного вида разработаны специальные методы математического программирования (не путать с компьютерным программированием): линейного программирования, целочисленного программирования и т. д.