Точки перегиба кривой

Точку, лежащую на кривой10 называют точкой перегиба, если она отделяет участок выпуклости кривой от участка вогнутости (рис. 4.16.4).

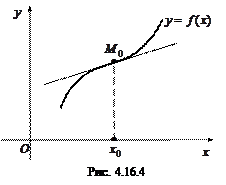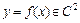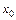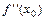Если функция , т.е. дважды непрерывно дифференцируема, то по одну сторону от точки перегиба f ''(х) < 0, а по другую f ''(х) > 0. Следовательно, для абсциссы точки перегиба имеем =0. Таким образом, точки перегиба находятся среди точек с такими абсциссами 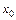, для которых 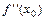= 0 или 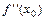не существует.

Это условие является необходимым, но не достаточным. Достаточное условие состоит в том, чтобы производная f "(x)при переходе через значение 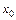изменяла свой знак.

Очевидно, что кривая в точке перегиба переходит с одной стороны касательной на другую, т.е. величина 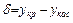должна изменять свой знак. Поскольку

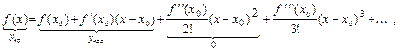то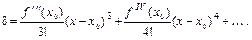

Если 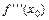¹0, то 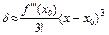и d изменяет знак при переходе х через значение 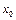, т.е. имеем точку перегиба с абсциссой .

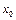Если 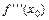=0, 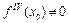, то d знака не изменяет и точки перегиба не будет:

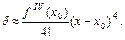
Отсюда ясно, что достаточное условие точки перегиба состоит в том, что младшая из производных 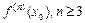, отличных от нуля, имеет нечетный порядок. Это согласуется с уже выполненным анализом стационарных точек: если m — четное, то в стационарной точке будет экстремум, если m — нечетное, то стационарная точка отвечает точке перегиба.

П р и м е р

.

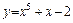Находим абсциссы возможных точек перегиба:

.

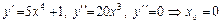Проверяем это значение:

,

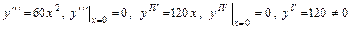т.е. 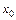= 0 отвечает точке перегиба.