Экстремумы функции. Пусть = 0, а ¹ 0. Тогда вблизи точки
Пусть 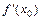 = 0, а
= 0, а 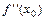 ¹ 0. Тогда вблизи точки
¹ 0. Тогда вблизи точки 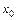
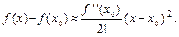
Так как 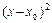 ³ 0, то знак разности f (x) –
³ 0, то знак разности f (x) – 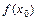 всецело определяется знаком второй производной
всецело определяется знаком второй производной 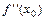 :
:
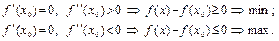
Аналогично рассматривается случай, когда
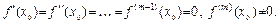
Здесь вблизи точки x0
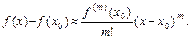 (4.16.3)
(4.16.3)
Неизменность знака правой части равенства (4.16.3) возможна лишь в том случае, когда m — четное число. Поэтому справедлив следующий вывод: если наименьший порядок m производной, отличной от нуля в точке 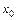 , является четным, то в точке
, является четным, то в точке 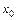 функция имеет экстремум (при
функция имеет экстремум (при 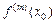 > 0 — минимум, при
> 0 — минимум, при 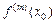 ) < 0 — максимум). Если m — нечетное число, то экстремума в точке
) < 0 — максимум). Если m — нечетное число, то экстремума в точке 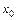 не будет (рис. 4.16.2).
не будет (рис. 4.16.2).
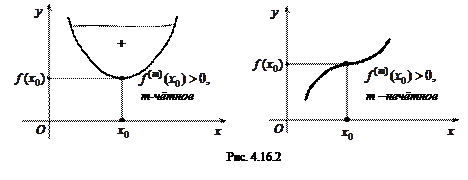
Пусть, например, требуется найти экстремум функции
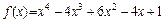 .
.
Для решения этой задачи последовательно вычисляем
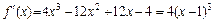 ;
;
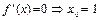 ;
;
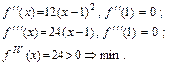
Результат можно было предвидеть, если учесть, что 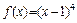 .
.
Дата добавления: 2015-10-19; просмотров: 592;
