Формула Тейлора для числовой функции нескольких переменных

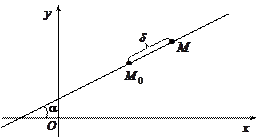Рассмотрим функцию двух переменных 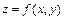, которая имеет все необходимые производные.

Выберем на плоскости точку 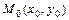и проведем через нее прямую (см. рисунок):

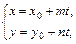
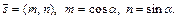Тогда расстояние от точки 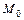до произвольной точки 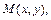лежащей на этой прямой,

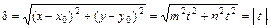
Отсюда, полагая, что 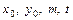зафиксированы, получаем функцию одной переменной t (функцию точки М на выбранной прямой линии):

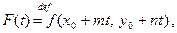
для которой нетрудно записать формулу Тейлора в окрестности точки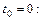

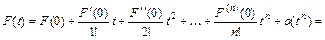
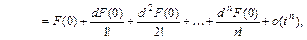(4.17.1)

так как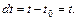

Для вычисления производных 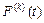вспомним, что

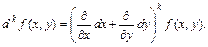
Так как здесь x = x(t), y = y(t), то, разделив на 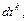получаем

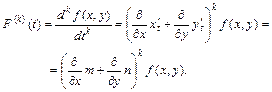
Вычислим, например, дифференциалы первого и второго порядка

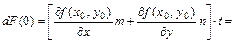
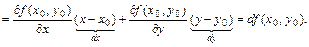
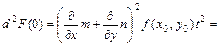
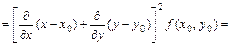
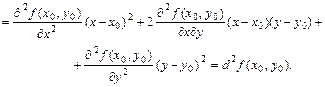
Поэтому вместо (4.17.1) можно записать

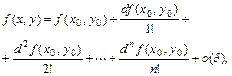(4.17.2)

где 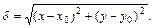Выражение (4.17.2) представляет собой формулу Тейлора для числовой функции двух переменных. Аналогично можно записать формулу Тейлора и в случае любого количества переменных.