Выпуклость и вогнутость кривой
 |
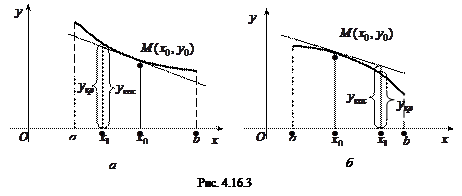Рассмотрим кривые, изображенные на рис. 4.16.3. Пусть для произвольной точки М лежащей на кривой, построена касательная к этой кривой. Если обозначить ординату точки на кривой через yкр, а соответствующей (т.е. имеющей ту же абсциссу
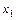) точки на касательной — через yкас, то можно рассмотреть разность 
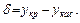(4.16.4)
Если d > 0 для любых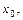 
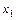Î(a, b), 
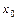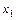¹ , то это означает, что на интервале (a, b) кривая лежит «не ниже» любой из своих касательных. Такая кривая называется вогнутой (выпуклой вниз) (рис. 4.16.3 а). Если d < 0, то кривая называется выпуклой (выпуклой вверх) (рис. 4.16.3 б).
Оказывается, что знак выражения (4.16.4) очень просто устанавливается с помощью формулы Тейлора:
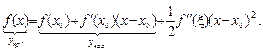(4.16.5)
Из (4.16.5) сразу следует, что при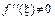 
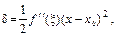
откуда имеем
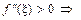вогнутость 
;
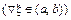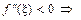выпуклость 
.
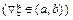Дата добавления: 2015-10-19; просмотров: 885;