Эпидемия болезней

В изолированном поселке с населением m человек возникла эпидемия болезни, распространение которой описывается соотношениями:

xi+1 = xi – b*xi*yi;

yi+1 = yi - cyi + bxi*yi;

zi+1 = zi + cyi;

x0=a0, y0=b0, z0=c0,

где xi, yi, zi - число здоровых, больных (инфицированных) и невосприимчивых (переболевших) в момент времени i=0.1...n;

b - частота контактов больных и здоровых;

c - величина, обратная среднему времени выздоровления и зависящая от эффективности лекарств 0<L<1.

Более строго соотношение может быть получено из системы дифференциальных уравнений:

Модель “хищник - жертва”

Имеются популяции двух видов, которые представляются отношениями

xi+1 = xi + a1xi - b1xi2 - g1xiyi , x0 = c1,

yi+1 = yi - a2yi + b2yi2 - g2xiyi , y0 = c2,

где xi - численность (плотность) жертв,

yi - численность хищников,

g1 - коэффициент защиты жертв,

g2 - коэффициент прожорливости хищников.

Рост опухоли

Раковая опухоль обычно увеличивается экспоненциально в соответствии с дифференциальным уравнением:

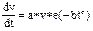
, где v - размер опухоли,

с,a,b - константы.

Определить, при каких значениях параметров С существует предельный размер опухоли. Выяснить, при каких значениях С рост опухоли не превосходит некоторой конечной величины.

1. Изучить характер эволюции популяции, при зна­чениях параметров a, b, n в зависимости от значения параметра b в диапазоне 0,1 < b < 10,

Есть ли качественные различия в характере эволюции в зависимости от значе­ния b?

2. Изучить характер эволюции популяции при зна­чениях параметров b, a, n в зависимости от значения параметра aв диапазоне 1 < a < 10,

Есть ли качественные различия в характере эволюции в зависимости от значе­ния a?

3. Изучить характер эволюции популяции а, b,v в зависимости от значения параметра V в диапазоне 1 <v<10.

Есть ли качественные различия в характере эволюции в зависимости от значе­ния v?

4. Реализовать модель при различных наборах значений параметров: n, a, b и изучить влияние параметров на характер эволюции.

5. Для модели в фазовой плоскости (b, a) найти границы зон, разделяю­щих режимы монотонного и колебательного установления стационарной числен­ности популяции изучаемой системы.

6. Для модели в фазовой плоскости (a,b) найти границы зон, разделяю­щих режим колебательного установления стационарной численности популяции изучаемой системы и режим устойчивых предельных циклов.

7. Реализовать моделирование межвидовой конкуренции по формулам при значениях параметров r1 = 2,r2= 2,k1 = 200, k2 = 200, a12 = 0,5,a21= 0,5. Проана­лизировать зависимость судьбы популяций от соотношения значений их началь­ной численности n1,n2.

8. Реализовать моделирование межвидовой конкуренции по формулам при значениях параметров r1 = 2,r2 = 2, k1 = 200, k2= 200, a12= 100, a21 = 100. Проанализировать зависимость судьбы популяций от соотношения значений ко­эффициентов конкуренции a12, a21,.

9. Построить в фазовой плоскости (n1n2) границы зон, разделяющих какие-либо два режима эволюции конкурирующих популяций (в соответствии с моделью ). Остальные параметры модели выбрать произвольно. Учесть при этом, что режим устойчивого сосуществования популяций может в принципе реализовать только при ф12 < 1.

10. Провести моделирование динамики численности популяций в системе «хищник-жертва» при значениях параметров r = 5, a= = 0, q = 2 c= 0,6 Проанализировать зависимость исхода эволюции от соотношения значений пара­метров n, c0.

11. Провести моделирование динамики численности популяций в системе «хищ­ник—жертва» при значениях параметров r = 5, а = 0,1, q = 2, f = 100, Со = 6. Проанализировать зависимость результатов моделирования от значения параметра a в диапазоне 0,1 : 2.

12.Провести моделирование динамики численности популяций в системе «хищ­ник—жертва» при значениях параметров r = 5, а = 0,1, f= 2, N = 100,

13. Провести моделирование динамики численности популяций в системе «хищ­ник—жертва» при значениях параметров а = 0,! f= 2, q = 2, N= 100, Со=б. Проанализировать зависимость результатов моделирования от значе­ния параметра r в диапазоне 0,1 < r < 2.

14. Провести моделирование динамики численности популяций в системе «хищ­ник—жертва» при значениях параметров a, q, No ,Co. Проанализировать зависимость результатов моделирования от значе­ния параметра «а» в диапазоне 0,1 < а < 2.

15.Модель «хищ­ник—жертва» предсказывает сопряженные колебания численности жертв и хищников. Исследовать зависимость запаздывания амплитуд колебаний числен­ности хищников от амплитуд колебаний численности жертв в зависимости от значений параметра а. Значения остальных параметров фиксировать по усмотре­нию.

16. Модель «хищ­ник—жертва» предсказывает сопряженные колебания численности жертв и хищников. Исследовать зависимость запаздывания амплитуд колебаний числен­ности хищников от амплитуд колебаний численности жертв в зависимости от значений параметра q. Значения остальных параметров фиксировать по усмотре­нию.

17.Модель предсказывает сопряженные колебания численности жертв и хищников. Исследовать зависимость запаздыванияамплитуд колебаний численно­сти хищников от амплитуд колебаний численности жертв и зависимости от значе­ний параметра a. Значения остальных параметров фиксировать по усмотрению.

18. Модель предсказывает сопряженные колебания численности жертв и хищников. Исследовать зависимость запаздывания амплитуд колебаний численно­сти хищников от амплитуд колебаний численности жертв в зависимости от значе­ний параметра f, Значения остальных параметров фиксировать по усмотрению.

19.Модель предсказывает сопряженные колебания численностижертв ихищников. Исследовать зависимость запаздывания амплитуд колебаний численно­сти хищников от амплитуд колебаний численности жертв в зависимости от соот­ношения значений начальных численностей популяции N0, С0. Значения осталь­ных параметровфиксировать по усмотрению.

23.Промоделировать процесс распространения инфекции стригущего лишая по участку кожи размером n*n (п — нечетное) клеток.

1.Внутривидовая конкуренция в популяции с

дискретным размножением Одна из центральных задач при моделировании случайных процессов — на­хождение характеристик случайных величин, являющихся объектом моделирова­ния. Главная такая характеристика — функция распределения. Ее вид можно каче­ственно оценить по гистограмме, построенной входе моделирования, а гипотезу офункциональной форме . Однако это не всегда целесообразно, особенно если в задаче требуется определить лишь неко­торые характеристики случайной величины — чаще всего среднее значение и дис­персию. Их можно найти без моделирования самой функции распределения проверить с помощью одного из стандартных критериев, используемых в математической статистике. При этом статистическая оценка достоверности результатов является обязательной.

Результаты моделирования уместно выводить на экран компьютера в следую­щем виде: в виде таблиц значений рассчитываемой величины (как правило, в нескольких выборках), в виде гистограмм распределения случайных величин, по­строенных в ходе моделирования.

Целесообразно там, где это возможно, сопровождать имитационное модели­рование визуальным отображением соответствующего процесса на экране компь­ютера (процесс формирования очереди, рождение и исчезновение объектов в за­дачах моделирования популяций и т.д.).