Пример 1
figure(1); //вызов графического окна;
clf; //очистка фигуры;
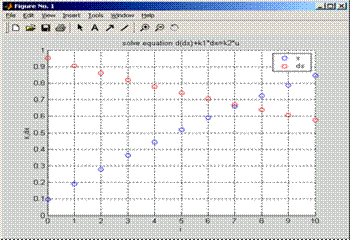
title(“solve equation d(dx)+k1*dx=k2*u”); //установка титульной надписи
syms k1 k2 p t T i Y01 Y02; //задание переменных;
//ввод данных;
k2=0.01;
k1=0.5;
//ввод исходных матриц;
B=[0 1;0 -k1];
U=[0.1];
E=eye(size(B)); //создание единичной матрицы
A=[0;k2];
D=E*p;
W=D-B;
W1=inv(W); //нахождение обратной матрицы
W2=ilaplace(W1,p,t); //обратное преобразование Лапласа
H=(int(W2,t,0,T))*A; //матрица управления
Y0=[Y01;Y02]; //матрица начальных условий
Y01=0;Y02=1;
W21=ilaplace(W1,p,T); //матрица состояния
T=0.1; // такт работы
for i=0:10,
Y=W21*Y0+H*U; //расчетная формула
Y1=Y01+(-2*exp(-1/2*T)+2)*Y02+1/500*T+1/250*exp(-1/2*T)-1/250;
Y2=exp(-1/2*T)*Y02-1/500*exp(-1/2*T)+1/500;
Y01=Y1; Y02=Y2;
hold on;.//обеспечение продолжение вывода графиков в текущее окно
plot(i,Y01,’o’,i,Y02,’or’);//построение графиков
legend(“x”,’dx’); //добавление к текущему графику легенды
xlabel(“i”); //установка надписи на оси OX
ylabel(“x,dx”); //становка надписи на оси OYgrid on; //сетка
end
Y2=exp(-1/2*T)*Y02-1/500*exp(-1/2*T)+1/500;
Y01=Y1; Y02=Y2;
hold on;.//обеспечение продолжение вывода графиков в текущее окно
plot(i,Y01,’o’,i,Y02,’or’);//построение графиков
legend(“x”,’dx’); //добавление к текущему графику легенды
xlabel(“i”); //установка надписи на оси OX
ylabel(“x,dx”); //становка надписи на оси OYgrid on; //сетка
end
нач. Условия
k1=0.5, k2=0.01; i=0..10; y10=0; y20=1; n=0.1; u=0.1

Y2=exp(-1/2*T)*Y02-1/500*exp(-1/2*T)+1/500;
Y01=Y1; Y02=Y2;
hold on;.//обеспечение продолжение вывода графиков в текущее окно
plot(i,Y01,’o’,i,Y02,’or’);//построение графиков
legend(“x”,’dx’); //добавление к текущему графику легенды
xlabel(“i”); //установка надписи на оси OX
ylabel(“x,dx”); //становка надписи на оси OYgrid on; //сетка
end
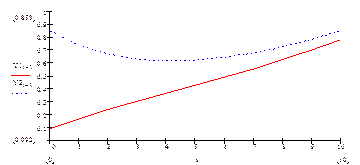
Пример. Для дифференциального уравнения



 С целью определения матриц уравнения параметров состояния преобразуем систему:
С целью определения матриц уравнения параметров состояния преобразуем систему:

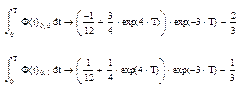
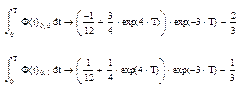
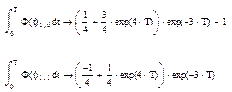
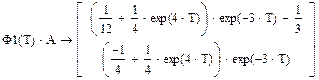
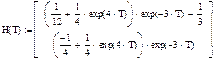
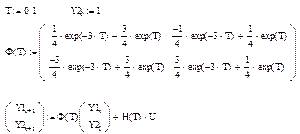
Дата добавления: 2015-09-07; просмотров: 615;
