Плоская электромагнитная волна с линейной поляризацией

Рассмотрим подробнее случай плоской волны. Это простейший вид волнового движения электромагнитного поля, имеющий, однако, большое значение для решения практических задач. Например, рассматривая сферические волны, возбужденные точечным источником, при достаточном удалении от него можно из-за малой кривизны заменить малый участок сферы плоскостью. Другими словами, плоские волны являются предельным случаем сферических волн при стремлении радиуса сферы к бесконечности. Аналогичная замена используется для случая цилиндрической волны.

Сделаем следующие предположения относительно рассматриваемой плоской волны:

1. Волна является плоской. Пусть волна распространяется вдоль оси 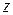, то есть комплексный вектор Пойнтинга направлен вдоль оси 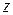, он имеет одну вещественную составляющую

,

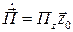откуда следует, что продольные (направленные вдоль оси 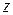) составляющие электрического и магнитного полей равны нулю:

, .

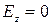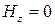2. Волна является однородной, т.е. амплитуды полей вдоль волнового фронта неизменны. Так как волновой фронт – плоскость, параллельная 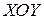, то это условие формулируется как

.

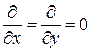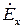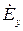3. Волна имеет линейную поляризацию. Это означает, что из двух возможных поперечных составляющих электрического вектора и только компонента 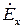отлична от нуля. Таким образом, вектор 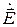колеблется параллельно оси 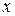в плоскости 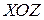. Эта плоскость называется плоскостью поляризации.

С учетом сделанных предположений система уравнений Гельмгольца относительно составляющих электрического вектора превращается в единственное уравнение

.

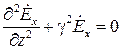В этом уравнении знак частной производной заменен на знак обыкновенной производной, поскольку неизвестная функция зависит лишь от координаты 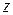. Общее решение данного уравнения имеет вид:

,

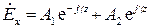где 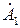, 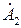− произвольные, вообще говоря, комплексные постоянные.

Сравнивая эту формулу с выражением для комплексных амплитуд плоской волны, убеждаемся, что она отображает сумму двух волн с одинаковыми постоянными распространения 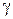, распространяющихся в разные стороны вдоль оси 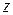. Первое слагаемое описывает падающую (прямую) волну, второе – отраженную (обратную) волну. Отраженная волна может возникнуть только при наличии неоднородности среды. Так как рассматривается однородная безграничная среда, то отраженная волна отсутствует. Положим тогда для определенност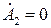и , и

.

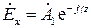Найдем магнитный вектор в данной плоской волне. Для этого воспользуемся вторым уравнением Максвелла

,

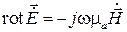откуда следует

.

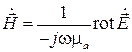Раскрывая операцию 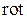, убеждаемся, что

.

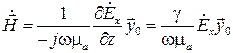Итак, вектор магнитного поля в данной плоской волне имеет лишь составляющую 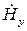и, следовательно, перпендикулярен вектору электрического поля.

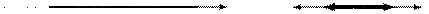
Рисунок 46 − Плоская волна в однородной среде без поглощения

Чрезвычайно важно отметить, что из этого уравнения следует, что между составляющими электрического и магнитного полей существует пропорциональность:

.

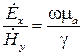Вывод, следующий отсюда состоит в том, что при отсутствии потерь в среде, т.е. при вещественном 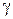, поля 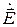и 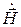колеблются в фазе. Это означает, что плоская электромагнитная волна в среде без потерь переносит только активную мощность.

Из теории линий с распределенными параметрами известно, что между напряжением 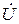и током 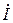в бегущей волне существует пропорциональность, причем 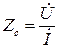называется характеристическим (волновым) сопротивлением данной линии. В аналогичной форме можно представить и вышеприведенное соотношение:

.

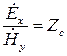Здесь 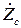−некоторая постоянная, имеющая размерность сопротивления и называемая характеристическим (волновым) сопротивлением данной среды. Из развернутого выражения для 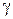следует, что

,

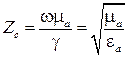т.е., 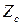полностью определяется лишь параметрами среды.

Параметром, очень важным для расчетов, является характеристическое сопротивление вакуума

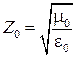
Подставив в эту формулу значения 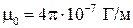и 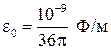, получим .

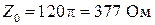Знание характеристического сопротивления данной среды позволяет находить электрическое поле в плоской волне по известному магнитному полю и наоборот.