Плоские волны в хорошо проводящих средах

Вопрос о распространении плоских волн в реальных металлах и металлоподобных средах рассмотрим более подробно из-за его практической важности. По определению с электродинамической точки зрения среда является хорошо проводящей, т.е., металлоподобной, если в каждой точке ее плотность токов проводимости 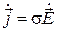значительно превосходит плотность токов смещения 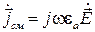. Это же условие металлоподобности может быть сформулировано в виде

,
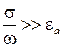т.е., мнимая часть комплексной диэлектрической проницаемости должна значительно превосходить вещественную часть.

Очевидно, что чем ниже частота 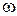, тем ближе при прочих равных условиях приближается данная среда к идеальному металлу. На достаточно низких частотах многие среды, известные как диэлектрики, становятся металлоподобными. Например, для сухой почвы с параметрами 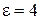, 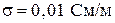на частоте 1 МГц имеем 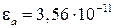, 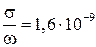. Таким образом, на частотах радиовещательных диапазонов сухая почва ведет себя подобно металлу. Такое свойство в ряде случаев позволяет значительно упростить решение практических задач.

Согласно сделанному предположению, комплексную диэлектрическую проницаемость металлоподобной среды можно считать мнимой:

.

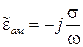Найдем комплексную постоянную распространения плоских электромагнитных волн в такой среде. По общему правилу,

.

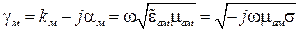Поскольку 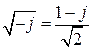, то выражение можно переписать в виде

.

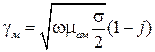Итак,

.

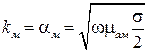Отсюда можно вычислить длину волны в хорошо проводящей среде:

.

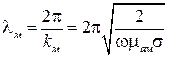Интересно отметить, что длина волны в металле значительно сокращается по сравнению с длиной волны в свободном пространстве. Действительно, легко вычислить, что

.

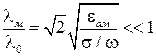Согласно этому неравенству, в металле значительно снижается фазовая скорость плоских электромагнитных волн.

Как известно, амплитуда электромагнитных волн в среде с потерями уменьшается по закону 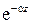. Расстояние 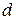, на котором амплитуда электромагнитных волн падает в е раз по сравнению с ее начальным уровнем, называется глубиной проникновения или глубиной поверхностного слоя (скин-слоя). Эта величина удовлетворяет соотношению

.

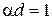Рисунок 48 − Глубина проникновения

Пользуясь вышеприведенными соотношениями, будем иметь

.

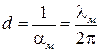Таким образом, приходим к другому определению: металлоподобной называется среда, в которой поле затухает на расстоянии, меньшем одной длины волны. Формула для вычисления глубины поверхностного слоя имеет следующий вид:

,

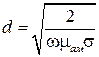т.е., глубина проникновения электромагнитных волн в металл уменьшается с ростом частоты и его удельной объемной проводимости.

Конкретный расчет по этой формуле показывает, что для металлов на частотах СВЧ диапазона величина 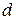оказывается весьма малой. Так, для меди, у которой 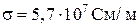, на частоте 10 ГГц (длина волны 3 см) имеем 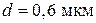. Отсюда следует важный для практики вывод об использовании нанесенного на поверхность конструкции слоя хорошо проводящего вещества, например серебра толщиной порядка 0,01 мм. Такое проводящее покрытие позволяет просто и дешево выполнять элементы СВЧ устройств с малыми тепловыми потерями.