Фазовая скорость и постоянная затухания плоских волн

В данном разделе на основе приведенных общих положений мы получим характеристики распространения плоских электромагнитных волн в некоторых наиболее важных средах.

Вакуум. Фазовая скорость волн в вакууме находится по общей формуле

.

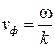Поскольку фазовая постоянная волн в вакууме

,

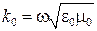фазовая скорость определится как

.

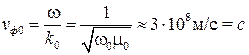Таким образом, получен один из основных результатов теории Максвелла − отождествление скорости света в вакууме со скоростью произвольной электромагнитной волны. Другими словами, скорость плоских электромагнитных волн в вакууме равна скорости света 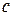независимо от частоты этих волн. В физике среды с подобными свойствами носят название сред без дисперсии.

Диэлектрик без потерь. Рассматривая случай немагнитного диэлектрика с 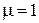, что часто встречается на практике, будем иметь

.

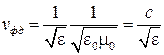Таким образом, фазовая скорость, а следовательно, и длина волны в диэлектрике уменьшаются в 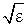раз по сравнению с аналогичными величинами, вычисленными для вакуума:

.

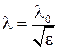Диэлектрик с потерями. Для анализа распространения волн в данной среде нужно воспользоваться понятием комплексной диэлектрической проницаемости

,

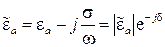где

, .

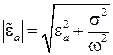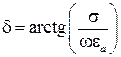Комплексная постоянная распространения в этом случае запишется следующим образом:

.

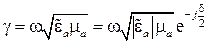Поскольку 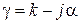, раскрывая это выражение по формуле Эйлера, будем иметь значение фазовой постоянной

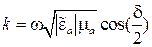
и постоянной затухания

.

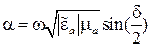Как уже указывалось, реальные диэлектрики характеризуются весьма малыми углами потерь, порядка 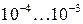, в силу чего с точностью до величин порядка 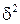можно считать, что

, , .

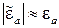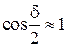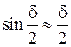Отсюда

,

,

.

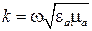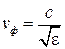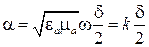Вывод, следующий из этих формул, состоит в том, что при расчете фазовых соотношений в первом приближении можно не учитывать потерь в материале. С другой стороны, коэффициент затухания плоских волн в неидеальном диэлектрике прямо пропорционален углу диэлектрических потерь.

Рисунок 47 − Плоская волна в среде с потерями